Svjetlost je val elektromagnetne prirode koji se u vakuumu prostire brzinom približno jednakom od c = 3 ¢ 108m/s . Prema Maxwellovoj teoriji elektromagnetizma, svjetlost je transverzalni val, tj. vektori električnog i magnetnog polja osciluju u ravnima koje su okomite na pravac prostiranja (slika 1.)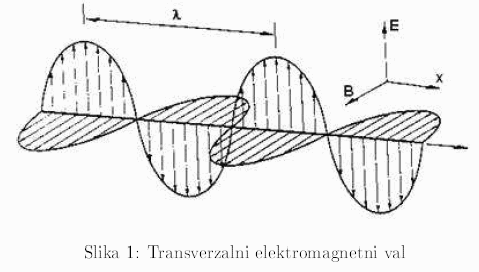

Postoje tri osnovne osobine elektromagnetnih valova:

1. interferencija,
2. difrakcija,
3. polarizacija.

Interferencija i difrakcija su svojstvene svim vrstama valova, kako mehaničkim tako i elektromagnetnim. Interferncija predstavlja slaganje dva ili više valova, a kao rezultat toga nastaju interferentne pruge koje se obično posmatraju na nekom zastoru.

Kod svjetlosnih valova interferentne pruge predstavljaju niz boja na zastoru u slučaju interferencije bijele svjetlosti, a u slučaju interferencije monohromatske, niz tamnih i svijetlih pruga koje se međusobno ponavljaju. Na mjestima svijetlih pruga, intenzitet svjetlosti usljed interferencije je maksimalno pojačan (konstruktivna interferencija), a na mjestima tamnih pruga, intenzitet je maksimalno oslabljen (destruktivna interferencija). Ova pojava se može uočiti na naftnim mrljama na vodi, pri čemu vidimo različite boje koje nastaju usljed interferencije bijele svjetlosti koja se odbije o gornju granicu i svjetlosti koja se odbije o donju granicu sloja nafte. Pojava zaobilaženja prepreka, odnosno ogibanja od strane valova naziva se difrakcija. Difrakcije se obično opaža kod zvučnih valova u slučaju kada slušaoc može da čuje svog sagovornika iako se on nalazi iza ugla. Ovu osobinu pokazuju i svjetlosni valovi kada nailaze na prepreke reda veličine valne dužine. S obzirom da je valna dužina svjetlosti reda 0; 4¹m¡0; 8¹m, difrakcija svjetlosti se ne opaža u normalnim uslovima. Polarizacija je osobina koju pokazaju samo elektromagnetni valovi. Naime, oscilacije električnog vektora kod bijela svjetlosti koja nastaje u atomskim procesima nisu uređenje, nego električno polje može da osciluje u ma kojoj ravni koja je okomita na pravac prostiranja vala. Za ovakav val kažemo da je nepolarizovan. Ako vektor eletktričnog polja osciluje samo u jednoj ravni, onda je riječ o polarizovanoj svjetlosti.

OPŠTI OBLICI INTERFERENCIJE SVJETLOSTI

TRAJNI EFEKTI INTERFERENCIJE SVJETLOSTI MOGU SE DOBITI SAMO SA KOHERENTNOM SVJETLOŠCU. ZA OBIČNE IZVORE SE UZIMA SVJETLOST SA JEDNOG SVJETLOSNOG IZVORA I PODESNIM POSTUPCIMA SE DOVODI U OKOLNOSTI POD KOJIMA SE MOŽE JAVITI INTERFERENCIJA. KOHERENTNA SVJETLOST IZ JEDNOG SVJETLOSNOG IZVORA SE RAZDVAJA NA DVA DIJELA KOJA, POŠTO PREDU RAZLIČITE PUTEVE PONOVO BIVAJU SPOLJENI. KAD SE SVJETLOST ODBIJA OD OPTIČKI GUŠCE SREDINE MJENJA SE FAZA TALASA ZA UGAO ı (180), DOK SE PRI ODBIJANJU OD OPTIČKI REDE SREDINE NE VRŠI OVA PROMJENA, ODNOSNO SVJETLOST SE ODBIJA SA ISTOM FAZOM OSCILACIJE. INTERFERENCIJA SVJETLOSTI SE MOŽE JAVITI ONDA KAD OBA ZRAKA PRELAZE JEDNAKE GEOMETRIJSKE DUŽINE PUTEVA, ALI UZ RAZLIČITE OPTIČKE DUŽINE, ODNOSNO AKO PROLAZE KROZ DVIJE OPTIČKE SREDINE RAZLIČITIH OPTIČKIH GUSTINA. OPISANI EFEKTI INTERFERENCIJE SA OBIČNOM MONOHROMATIČNOM SVETLOŠCU MOGU DA SE JAVE SAMO AKO RAZLIKA PUTEVA s2-s1 <OD 25CM.

FRESNELOVI OGLEDI INTERFERENCIJE SVJETLOSTI

MONOHROMATSKI SVJETLOSNI IZVOR SE NALAZI U S ISPRED DVA OGLEDALA O1 I O2, KOJA MEĐUSOBOM ZAKLAPAJU VRLO MALI UGAO DELTA SA DONJE STRANE JE SVJETLOSNI IZVOR ZAKLONJEN ZASTOROM Z, KOJI SPREČAVA DA DIREKTNA SVJETLOST IZ IZVORA NE OMETA EFEKTE INTERFERENCIJE U POLJU ISPOD OGLEDALA. IZ SVJETLOSNOG IZVORA S SE ŠIRE SVJETLOSNI TALASI PO KONCENTRIČNIM SFERAMA I PADAJU NA OBA OGLEDALA. POSLIJE ODBIJANJA OD OGLEDALA SVJETLOST SE I DALJE ŠIRI PO SFERAMA, KAO DA DOLAZE IZ TAČAKA S1, S2 KOJE PREDSTAVLJAJU LIKOVE IZVORA S U JEDNOM I DRUGOM OGLEDALU. TAKO SE SVJETLOST PO ODBIJANJU ŠIRI DALJE KAO KADA BI DOLAZILA IZ DVA SVETLOSNA IZVORA S1 I S2. SVJETLOST IZ S1 I S2 STVARNO POTIČE IZ ISTOG IZVORA S, TE I POSLIJE ODBIJANJA IMAMO KOHERENTNU SVJETLOST KOJA POD OPISANIM USLOVIMA MOŽE DA DAJE TRAJNE EFEKTE INTERFERENCIJE.

Interferencija svjetlosti

Interferencija je pojava koja nastaje na mjestima presijecanja valova koherentne svjetlosti. Ona predstavlja modifikaciju intenziteta dobivenu superpozicijom na mjestu presijecanja valova i opažamo je kao pojavu svijetlih i tamnih pruga na zaslonu. One su rezultat konstruktivne i destruktivne interferencije. Konstruktivna interferencija nastaje na mjestima gdje su valovi u fazi, a destruktivna gdje su valovi međusobno pomaknuti u fazi za

pa se brijeg jednog poklapa s dolom drugog vala i oni se poništavaju.
Razmotrimo interferenciju dvaju monokromatskih ravnih valova konstantnih amplituda, shematski prikazanu na slici (1).
Korištenjem kompleksne notacije dobivamo:

(1)

(2)
gdje je k=2

valni broj. Superpozicija tih valova u točki P daje svjetlosno polje:

(3)
odakle slijedi ukupni intenzitet, u1 (x)=|u (x)|2,

(4)
gdje su I1= u012 i I2= u022 pojedinačni intenziteti.
Rezultat konstruktivne interferencije je maksimum intenziteta (svijetla pruga) koji se dobije kada je razlika optičkih puteva jednaka višektratniku od

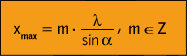(5)
Rezultat destruktivne interferencije je minimum intenziteta (tamna pruga) koji dobivamo za razliku puteva

/2 + višektratnik od

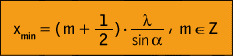(6)
Broj m određuje svijetlu prugu koja se naziva m-ti red interferencije. Vidljivost pruga interferencije (dubina modulacije) za savršeno koherentnu svjetlost ovisi samo o omjeru intenziteta I1 i I2 i najveća je za I1 = I2.

Za opisivanje valova koriste se funkcije cos i sin. Buduci da je svjetlost elektromagnetni val, oscilacije električnog polja možemo opisati kao

Gdje je

početna faza vala. Ako se faza vala ne mijenja u toku vremena onda kažemo da je val koherentan, u protivnom val je nekoherentan. Svjetlost koja se dobija zračenjem užarenih tijela (npr. sunčeva svjetlost) je izrazito nekoherentna, dok je laserska svjetlost izrazito koherentna. Pomocu nekohrentne svjetlosti ne može se dobiti interferentna slika. Razmotrimo sada slaganje dva vala opisana gornjom relacijom iste frekvencije ali različitih faza. Prvi val se prostire sredinom indeska prelamanja n1 , a drugi n2. U nekoj tački valovi interferiraju. Pojava svijetlih ili tamnih pruga na zastoru usljed interferencije najprije zavisi od intenziteta rezultuju¢ih oscilacija. Pokazuje se da je intenzitet rezultuju¢ih oscilacija jednak

gdje su I1 i I2 intenziteti prvog i drugog vala. Prema tome, ukoliko je dobijamo maksimalno pojačanje, a ukoliko je -1 dobijamo maksimalno slabljenje.

Thomas Youngov eksperiment interferencije

Prvi slučaj interferencije svjetlosti je dobijen u Youngovom eksperimentu iz 1802: godine. Postavka eksperimenta je prikazana na donjoj slici.
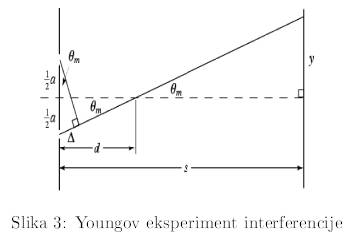
Youngov eksperiment interferencije

Svjetlosni izvor emituje nekoheretnu svjetlost koja pada na dvije pukotine koje su me.usobno udaljenje na rastojanju a. S obziriom da svjetlosni valovi istovremeno nailaze na obje pukotine, pukotine postaju izvori sekundarnih koherentnih valova. Uslov interferencije valova koji dolaze iz novih izvora je

Udaljenost proizvoljne tačke na ekranu je

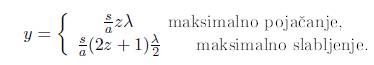
Prema tome, u tački koja je udaljena za y od sredine između pukotina nastaje konstruktivna, odnosno destruktivna interferencija ako je ispunjeno:

gdje je z redni broj maksimuma, odnosno minimuma.

Udaljenost između dva susjedna maksimuma ili dva susjedna minimuma je

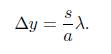
Interferencija svjetlosti na tankom prozračnom klinu

Svjetlost talasne dužine λ 0 pada normalno u odnosu na donju površinu klina malog nagibnog ugla θ. Klin je napravljen od materijala apsolutnog indeksa prelamanja n.
Usled interferencije na gornjoj površini klina će se pojaviti naizmenično raspoređene svjetle i tamne pruge.

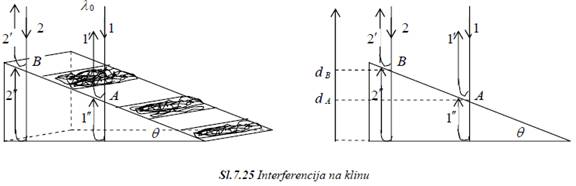
Interferencija svjetlosti na klinu
Posmatraćemo konstruktivnu interferenciju u tačkama A i B , tako da je u tački A konstruktivna interferencija reda z , a u tački B reda z +1. U tački A talas 1 dijeli se na reflektovani talas 1′′ i transmitovani, koji nakon refleksije od donje površine stiže kao talas 1′ do tačke A i interferenira sa talasom 1′ . Fazna razlika ova dva talasa je

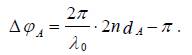
Do fazne razlike dolazi nakon razdvajanja talasa Talas 1′′ nakon razdvajanja pređe geometrijski put 2d A do ponovnog spajanja, a talas 1′ pošto se odbija od sredine koja ima veći apsolutni indeks prelamanja ima negativnu vrednost amplitude što odgovara promeni faze za
Kako se tačka A nalazi u oblasti konstruktivne interferencije (svjetla pruga) iz slijedi da je , tako da se svodi na

Za tačku B imamo da je

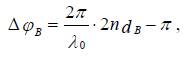
i pošto je u njoj sljedeći interferencioni maksimum

i dobijamo

Na osnovu toga imamo

Ako je rastojanje između dvije najbliže svjetle pruge L (a to je i rastojanje između dvije najbliže tamne pruge) onda je

Kako je θ mali ugao sinθ ≈θ . Uzimajući u obzir navedenu aproksimaciju dobijamo

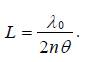
Pri rešavanju problema često se umesto rastojanja L daje veličina Tada L (izraženo u cm ) dobijamo iz relacije

Razlika između interferencije i difrakcije

Kada tačkasti izvor svjetlosti baca sjenku objekta na zastor, zakoni optike predviđaju da oštra razlika treba da se vidi između osunčenog djela i onog potpuno osvetljenog. Bliže ispitivanje pokazuje da ovo nije slučaj. Difrakcije se tiče devijacije od principa geometrijske optike. Svjetlost ne putuje uvijek pravo zato što objekat može uticati na krivljenje trajektorije svjetlosti. Huygens je predložio 1678. da svaka vibrirajuća tačka talasnog fronta postaje izvor novih poremećaja. Ovi sekundarni poremećaji formiraju omotač oko originalnog talasa i talas se propagira kroz sredinu.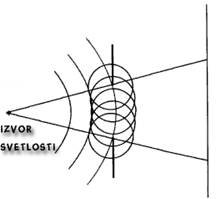
Razlika izmedju interferencije i difrakcije

Razlika izmedju interferencije i difrakcije

Ako stavimo prepreku u pravcu propagacije talasa, svjetlo daleko od prepreke nastavlja da se propagira netaknuto, ali blizu ivica sekundarni talasi ne nalaze kompenzujuću komponentu da se spoje sa njom u sjenci. Kao rezultat talasni front se savija oko ivice. Thomas Young je ispitao intezitet svjetlosti koja pada na zastor kada svjetlost iz jednog izvora prolazi kroz dve paralelne pukotine. Posmatrao je takođe dobijenu sliku i koristeći Huygensov princip, obrazložio je superpozicijom talasa koji kreću sa 2 pukotine koje se ponašaju kao dva izvora svjetlosti u fazi. Prvi primer je difrakcije, drugi interferencija. U prvom primeru dobijena slika je rezultat superpozicije talasa koji dolaze sa različitih djelova istog talasnog fronta, dok u potonjem slučaju dobijena slika rezultuje od superpozicije talasa iz dva različita talasna fronta. Tako jasno odvojena slika difrakcije i interferencije se retko pronalazi. Česti su slučajevi učešća fenomena difrakcije pri interferenciji i obrnuto.

MICHELSONOV INTERFEROMETAR

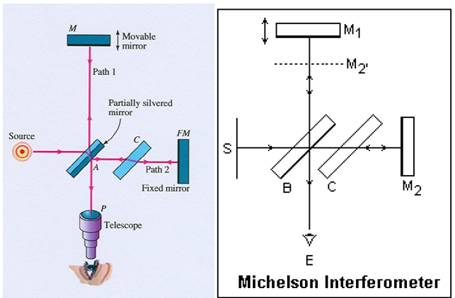
To je uređaj kojim se može promatrati interferencija dvaju snopova svjetlosti.

Izvor svjetlosti – monokromatski – iz He-Ne lasera snop prolazi kroz dvije leće (prva proširuje snop, druga ga kolimira) – pada na djelitelja snopa (polupropusna plocica koja zatvara kut od 45º sa zrcalima Z1 i Z2) – dio snopa se propusti do Z1, a dio reflektira do Z2.
Svjetlo se reflektira na Z1 i Z2 i vraca prema djelitelju snopa gdje otprilike pola energije ide prema zastoru, a druga polovina natrag u izvor.
Na zastoru promatramo interferencijske pojave.

NEWTONOVI KOLOBARI

Newtonova stakla se sastoje od planparalelne staklene ploče i na nju postavljene plankonveksne leće vrlo velikog polumjera zakrivljenosti R.
Kad na plankonveksnu leću pada monokromatska svjetlost, zbog djelomične refleksije dolazi do stvaranja geometrijske razlike hoda izmedu 2 vala koji onda mogu interferirati.

NEWTONOVI KOLOBARI U REFLEKTIRANO SVJETLOSTI

Svjetlosni val se nakon djelomične refleksije u tački A dijeli na:
- zraku 1 koja se reflektira u tocki A natrag
- zraku 2 koja nastavlja put do planparalelne ploče i tamo se reflektira prijeđe 2 puta udaljenost AB = d i pri tom reflektira na optički gušćem sredstvu indeksa loma n) pa je ukupna razlika faza:

Tačka dodira leće i planparalelne ploče je tamna – nulti prsten je taman – geometrijska razlika hoda = 0 (odn. d = 0), ali poništavanje nastaje zbog promjene u fazi za p zrake koja se reflektira na donjoj dodirnoj površini.

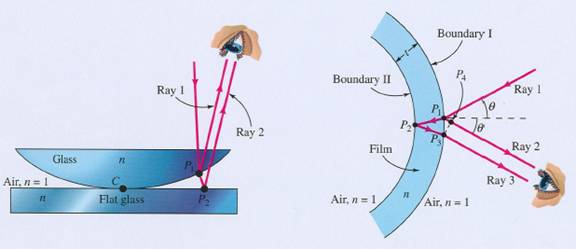
NEWTONOVI KOLOBARI U TRANSMITIRANOJ SVJETLOSTI

Zraka 2 se dva puta reflektira na optički gušcem sredstvu: jednom na planparalelnoj ploči, drugi put na donjoj, zakrivljenoj površini leće – ukupna promjena u fazi zbog refleksije jednaka je 2p - nema promjene u razlici faza – tamni prstenovi su postali svijetli i obrnuto.
Dodirna tačka je svijetla jer je geometrijska razlika hoda jednaka 0, a dodatne faze nema.

INTERFERENCIJA U TANKIM PROVIDNIM LISTOVIMA

POJAVE RAZLIČITIH BOJA NA TANKIM PROVIDNIM LISTOVIMA OSVETLJENIM BIJELOM SVETLOŠĆU RECU SE ČESTO PRI RAZLIČITIM OKOLNOSTIMA. SLIČNE POJAVE SE MOGU DETALJNIJE POSMATRATI POMOČU OPNE OD SAPUNICE NAČINJENJE NA EDNOM PRAVOUGAONOM RAMU OD ŽICE. UZIMAMO TANAK PROVIDNI LIST SA PARALELNIM GRANIČNIM POVRŠINAMA PUSTIMO, NAJPRIJE SAMO JEDAN SVJETLI ZRAK POD IZVJESNIM UGLOM PREMA NORMALI NA POVRŠINU. POZNATO JE DA SE SVJETLOST U OVAKVOM SLUČAJU DJELOM ODBIJA, A DJELOM PROLAZI KROZ PROZRAČNI LIST SE OD JEDNOG UPADNOG ZRAKA OBRAZUJE VIŠE ODBIJENIH ZRAKA. ZRACI 1 I 2 POTIČU OD ISTOG KOHERENTNOG UPADNOG ZRAKA, A IMAJU RAZLIČITE OPTIČKE PUTANJE.
ODBIJENI ZRAK ĆE SE ODBITI POD ISTIM UGLOM PREMA NORMALI. ZRAK KOJI ULAZI U LIST SLIJEDI ZAKONIMA PRELAMANJA I IZAĆI ĆE IZ LISTA U ISTOM PRAVCU SAMO POMJEREN ZA IZVJESNO MALO RASTOJANJE. ODBIJANJE SE JAVLJA I NA DONJOJ POVRŠINI, ODNOSNO PRI PRELAZU ZRAKA IZ OPTIČKI GUŠČE U OPTIČKI REDU SREDINU. OD OVE POVRŠINE ODBIJENI ZRAK OPET PADA NA GORNJU GRANIČNU POVRŠINU GDJE SE DJELOM OPET ODBIJA, A DJELOM PROLAZI U VAZDUŠNI PROSTOR IZNAD LISTA. PROCES DJELIMIČNOG ODBIJANJA SE I DALJE NASTAVLJA, PA SE OD JEDNOG UPADNOG ZRAKA OBRAZUJE VIŠE ODBIJENIH ZRAKA. ZRACI 1 I 2 POTIČU OD ISTOG KOHERENTNOG UPADNOG ZRAKA, A IMAJU RAZLIČITE OPTIČKE PUTANJE.

Koherencija svjetlosti

Svjetlost je koherentna ako među fotonima postoji konstantan ili predvidiv fazni odnos, pri čemu se koherencija manifestira kao prostorna i vremenska.
Kod prostorne koherencije promatra se fazni odnos valova na različitim mjestima u prostoru u isto vrijeme (Youngov eksperiment), dok se kod vremenske koherencije promatra fazni odnos valova na istom mjestu u prostoru ali u različitim vremenima (Michelsonov eksperiment).
Prema tome, tAčkasti izvor koji zrači svjetlost samo jedne frekvencije bio bi savršeno koherentan. Međutim, takav izvor ne postoji. Realni izvori se sastoje od velikog broja približno točkastih izvora (atomi) koji zrače svjetlost konačne spektralne širine pa nisu savršeno koherentni.

U slučaju lasera konfiguracija optičkog rezonatora može podržavati razne transverzalne i longitudinalne modove. Prostorna koherencija je najveća kada laser radi u TEM00 transverzalnom modu. Vremenska koherencija je to veća što je manji broj longitudinalnih modova prisutan u izlaznom snopu lasera, a najveća je kada je prisutan samo jedan longitudinalni mod.
Općenito, stupanj koherencije izmedu dvaju valova prostorno i vremenski razmaknutih označava se sa , a utječe na vidljivost pruga interferencije prema relaciji:

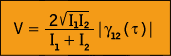
gdje su intenziteti valova označeni sa I1 i I2. Za jednake intenzitete snopova, vidljivost pruga jednaka je apsolutnoj vrijednosti stupnja koherencije pa se može direktno mjeriti.

Bilježenje i rekonstruiranje valne fronte

Laserski snop je podijeljen na snop koji direktno pada na fotoploču (referentni) i snop kojim osvjetljavamo objekt (objektni). Manipuliranjem snopova optičkim elementima (zrcala, leće, širitelji), dovodimo ih do fotoploče. Fotoploča bilježi interferenciju referentnog snopa i objektnog snopa. Optički putevi izmedu referentnog i objektnog snopa moraju biti jednaki. Zabilježena rešetka je oblika opisanog jednadžbom.
Radovima Huygensa, Fresnela, Younga i drugih dokazana je valna priroda svjetlosti. Međutim, pojavu kao što je npr. fotoelektrični efekt možemo objasniti postojanjem svjetlosne čestice - fotona. U okviru projekta KOHERENTNA OPTIKA razmatrat ćemo tipično valne pojave nastale kao rezultat interferencije i difrakcije valova koherentne svjetlosti. Dakle, opažanje, mjerenje i matematičko opisivanje pojava u koherentnoj optici temeljni je korak u razumijevanju procesa prijenosa i pretvorbe valne informacije.

Valni oblik i gibanje možemo si predočiti promatranjem površine vode na koju smo bacili kamen. Perturbacija mirne površine vode postaje izvor površinskih valova koji se djelovanjem gravitacije i pokretljivošću tekućine prenose dalje.

Na sličan način, kod svjetlosnih valova elektromagnetski podražaj prenosi se uslijed uzajamnog djelovanja električnog i magnetskog polja. Gibanje elektromagnetskih valova opisujemo valnom jednadžbom, čija rješenja najčešće opisuju kuglasti val (blizu izvora) ili ravni val (daleko od izvora). Najjednostavniji pristup (matematički i eksperimentalni) omogućuje upotreba izvora koherentne svjetlosti (laseri), pri čemu svjetlosnu valnu frontu moduliramo optičkim elementima kao što su leće, zrcala, širitelji i djelitelji snopova, itd.

LITERATURA

- Vernić - Mikuličić, Vježbe iz fizike, Školska knjiga, Zagreb, 1991.
- Mikuličić - Vernić, Praktikum eksperimentalne nastave fizike, Sveučilište u Zagrebu, 1966.
- Popularna enciklopedija, Sarajevo, 2001.
- Internet

PROČITAJ / PREUZMI I DRUGE SEMINARSKE RADOVE IZ OBLASTI:

preuzmi seminarski rad u wordu » » »

Besplatni Seminarski Radovi