OSTALI SEMINARSKI RADOVI
IZ FIZIKE:
|
||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||
Zračenje apsolutno crnog tijela – Plankov zakon
zračenja;
Fotoelektrični efekat – Ajnštajnovo zračenje fotoefekta
Idealno crno tijelo je tijelo koje upija sve talasne dužine elektromagnetnog zračenja, koje padaju na njega. Idealno crno tijelo ne postoji, ali ga može prilično dobro zamijeniti velika zatvorena šupljina sa malim otvorom i koja je toliko neprozirna da jedva odbija zračenje, budući da zračenje koje uđe u tu šupljinu, gotovo da nema šansu da izađe. Budući da idealno crno tijelo upija sve valne duljine bez gubitaka, ono isto emitira sve valne duljine bez gubitaka, ovisno samo o termodinamičkoj temperaturi tog tijela.
Toplinsko zračenje je elektromagnetno zračenje svih tijela koja se nalaze na temperaturi iznad apsolutne nule (0 K), odnosno odzračena energija ovisi samo o temperaturi promatranog tijela i stanju njegove površine. Primjer toplinskog zračenja je infracrveno zračenje koje emitiraju obični radijator ili električni grijač. Osoba u blizini vatre ili bilo kojeg drugog vrućeg tijela će osjetiti zračenje topline, čak i ako je okolni zrak jako hladan. Kako temperatura dalje raste, iznad 900 K, tijelo počinje žariti crvenu, zatim narančastu, žutu, bijelu i plavu boju. Kada se tijelo vidi bijelo, to znači da postoji znatan udio ultraljubičastog zračenja. Pripadajuće boje:
°C |
Pripadajuća boja |
480 |
zagasiti crveni sjaj |
580 |
tamno crvena |
730 |
izrazito crvena, skoro narandžasta |
930 |
tamno narandžasta |
1100 |
blijedo žuto narandžasta |
1300 |
žuto bijela |
> 1400 |
bijela (iz daljine žućkasta) |
Tabela 1. Pripadajuće boje zračenja
Svako tijelo ili materija, emituje elektromagnetsko zračenje kada je temperatura iznad apsolutne nule. Zračenje prestavlja pretvorbu toplinske energije tijela u elektromagnetnu energiju, i zato se zove toplinsko zračenje. Obratno, svako tijelo ili materija upija elektromagnetsko zračenje, do nekog stupnja. Kada tijelo upije cjelokupno zračenje, koje padne na njega, u cijelom rasponu valnih duljina, onda se ono naziva idealno crno tijelo. Kada idealno crno tijelo ima ravnomjerno raspoređenu temperaturu po površini, ono emitira karakterističnu raspodjelu frekvencija, koje ovisi o temperaturi. To se zove zračenje idealnog crnog tijela.
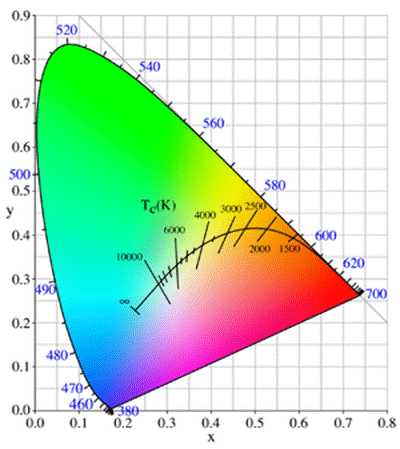
Slika 1. Boja zračenja idealnog crnog tijela ovisi
o temperaturi
Pojam crnog tijela je idealizirano, ono u stvarnosti ne
postoji. Ipak, grafit je vrlo dobro približenje idealnom crnom
tijelu. U labaratoriju, idealno crno tijelo se ostvaruje sa velikim krutim
tijelom koje ima šupljinu, koje ima mali otvor, jednoliko raspoređenu
temperaturu, kompletno je mutno i samo vrlo malo odbija svjetlost. Tako
recimo velika kutija, sa grafitnim zidovima, jednolike temperature i vrlo
malim otvorom, predstavlja vrlo dobro približenje.
Ako ima dovoljno veliku temperaturu, idealno crno tijelo počne žariti. Draperova
tačka je temperatura kada kruto tijelo počne tamno crveno svjetliti,
a iznosi 798 K (525˚ C). Kod 100 K otvor izgleda crven, a kada ima 6 000
K, izgleda bijelo. Kod većih temperatura, bila kakva peć, izrađena od
bilo kojeg materijala, je dobro približenje idealnog crnog tijela.
Ako postoje dva idealna crna tijela, onda će prema ravnotežnom stanju
zračenja, ukupni intenzitet zračenja koje neko tijelo emitira, bilo to
tijelo crno ili ne, biti jednako intenzitetu zračenja, koje to tijelo
upije.
Proračun krive zračenja idealnog crnog tijela, bio je jedan od glavnih
izazova u teorijskoj fizici 19. stoljeća.
PLANKOV ZAKON ZRAČENJA
 Problem
je rješio 1901. Max Planck, postavivši Planckov zakon za idealno
crno tijelo. Wienov zakon pomaka daje talasnu dužinu maksimalnog
intenziteta zračenja, a Stefan-Boltzmannov zakon određuje intenzitet
zračenja nekog tijela. Planck je pretpostavio da je energija oscilatora
unutar šupljine crnog tijela kvantizirana, a Eistein je
na osnovu minimalne kvantne energije elektromagnetnog zračenja, 1905.
objasnio fotoefekt, što je dovelo do pojave pojma fotona. To je dovelo
do pojave kvantne elektrodinamike, koja je zamijenila klasičnu teoriju elektromagnetizma.
Nakon toga se razvila raspodjela kvantne vjerovatnosti, ili Fermi-Diracova
statistika i Bose-Einsteinova statistika, gdje je svaka bila primjenjiva
za različite elementarne čestice, fermione i bozone.
Problem
je rješio 1901. Max Planck, postavivši Planckov zakon za idealno
crno tijelo. Wienov zakon pomaka daje talasnu dužinu maksimalnog
intenziteta zračenja, a Stefan-Boltzmannov zakon određuje intenzitet
zračenja nekog tijela. Planck je pretpostavio da je energija oscilatora
unutar šupljine crnog tijela kvantizirana, a Eistein je
na osnovu minimalne kvantne energije elektromagnetnog zračenja, 1905.
objasnio fotoefekt, što je dovelo do pojave pojma fotona. To je dovelo
do pojave kvantne elektrodinamike, koja je zamijenila klasičnu teoriju elektromagnetizma.
Nakon toga se razvila raspodjela kvantne vjerovatnosti, ili Fermi-Diracova
statistika i Bose-Einsteinova statistika, gdje je svaka bila primjenjiva
za različite elementarne čestice, fermione i bozone.
Stvarna tijela se neće ponašati kao idealno crno tijelo, već će to biti samo dio toga zračenja, a to se obilježava sa stepenom emisije (ε < 1), koji upoređuje realno sivo tijelo sa idealnim crnim tijelom. Stepen emisije ovisi o temperaturi, uglu emisije i valnoj duljini.
Idealno crno tijelo će emitovati zračenje na svim frekvencijama, ali one teže nuli kod visokih frekvencija. Tako na primjer, kod sobne temperature, na jedan kvadratni metar, idealno crno tijelo na sobnoj temperature (310 K), će emitovati foton u vidljivom dijelu spektra (390 – 750 nm), u prosjeku svake 41 sekunde, što za praktičnu primjenu znači da nema emisije vidljive svjetlosti.
Formula Plankovog zakona zračenja
Planckov zakon opisuje intenzitet (specifičnu snagu) zračenja nepolariziranog elektromagnetskog
zračenja, kod cijelog raspona talasnih dužina, kojeg emituje idealno crno
tijelo, ovisno o termodinačkoj temperaturi T:
![]()
gdje je:
I(ν,T) – intenzitet zračenja, ili energija po jedinici vremena,
po jedinici površine, s koje se emitira zračenje, po jedinici prostornog
ugla, po jedinici frekvencije ili valne duljine, idealno crnog tijela,
pri termodinamičkoj temperaturi
T, h – Planckova konstanta,
c – brzina svjetlosti u vakuumu,
k – Boltzmannova konstanta,
ν – frekvencija elektromagnetskog zračenja,
T – termodinamička temperature u Kelvinima.
Ta funkcija prestavlja snagu emitovanog zračenja idealnog crnog tijela
u smjeru normale, po jedinici prostornog kuta i po jedinici frekvencije.
Planckova raspodjela intenziteta zračenja je jedinstvena raspodjela, koja
može postojati u termodinamičkom ravnotežnom stanju.
Tijelo koje upija sve talasne dužine elektromagnetnog zračenja, koje padaju
na njega je idealno crno tijelo. Idealno crno tijelo ne postoji,
ali ga može prilično dobro zamijeniti velika zatvorena šupljina sa malim
otvorom i koja je toliko neprozirna da jedva odbija zračenje, budući da
zračenje koje uđe u tu šupljinu, gotovo da nema šansu da izađe. Budući
da idealno crno tijelo upija sve talasne dužine bez gubitaka, ono isto
emitira sve talasne dužine bez gubitaka, ovisno samo o termodinamičkoj
temperaturi tog tijela.
Planckov zakon vrijedi ako se zračenje promatra normalno na šupljinu idealnog
crnog tijela. Ako se promatra pod bilo kojim drugim kutem, onda je intenzitet
zračenja:
![]()
gdje je ugao θ između normale i pravca promatranja.
Vršna tačka ![]() je
za
je
za ![]()
Kao funkcija talasne dužine λ, Planckov zakon se može pisati
(po jedinici prostornog kuta steradijan) kao:
![]()
Tada je vršna tačka ![]() ,
a ona se obično izrazava sa Wienovim zakonom pomaka.
,
a ona se obično izrazava sa Wienovim zakonom pomaka.
Intenzitet zračenja za određeno područje frekvencija ![]() ,
], ili za određeno područje talasnih dužina
,
], ili za određeno područje talasnih dužina ![]() ,
se može dobiti integrisanjem funkcija:
,
se može dobiti integrisanjem funkcija:
![]()
Plankova kvantna hipoteza i zakon kvantizacije harmonijskog oscilatora
Eksperimantalni podaci ukazuju da apsolutno crno tijelo emituje veoma malo energije na malim talasnim dužinama, dok klasična teorija govori da energija treba da bude ravnomjerno raspoređena po svim talasnim dužnama. Da bi objasnio ovu neusaglašenost, Plank je pretpostavio da količina energije zavisi od talasne dužine te energije. Postavio jedve hipoteze:
- molekuli (tj. oscilatori) emituju energiju u zasebnim, izdvojenim količinama – zračenje je diskretno i emituje se iz tijela u ″paketićima″ koji sadrže tačno određenu količinu energije. Količina na latinskom – kvantum, pa je te tzv. ″paketiće″ Plank nazvao kvantima.
- Energija kvanta zavisi od talasne dužine emitovanog zračenja:
![]()
Molekuli (atomi, oscilatori) apsorbuju i emituju energiju koja može da bude jednaka SAMO cjelobrojnom umnošku energije jednog kvanta tj.:
![]()
Energija kvantnog oscilatora ima tačno određene, diskretne vrijednosti – ENERGIJA JE KVANTOVANA. Uvođenje zamisli da postoji kvant energije je bila prekretna tačka u razvoju kvantne fizike, iako je bilo potrebno mnogo vremena (preko 20 godina) da naučna javnost, pa i sam Plank prihvate dubinu tog otkrića. Kvantna teorija ne poništava dostignuća klasične fizike, već samo postavlja temelje sveobuhvatnijem opisivanju prirodnih pojava na svim nivoima i u svim oblastima. Fundamentalni zakoni kvantne fizike daju osnovu i potvrđuju važenje fenomenoloških zakona klasične fizike u granicama njihove primjenljivosti, povezujući ih na taj način u cjelinu.
FOTOELEKTRIČNI EFEKAT
Fotoelektrični efekat je
emisija elektrona iz metala pod dejstvom svjetlosti.
Otkrio ga je sasvim slučajno Herc 1887. godine. Prije Ajnštajna fizičare
je bunilo to što više svjetlosti izbija više elektrona ali im ne mijenja
energiju. Na energiju elektrona utiče boja (talasna dužina), a ne intenzitet
svjetlosti. Ajnštajn je sve nedoumice riješio 1905. godine pretpostavkom
da je svjetlost čestične prirode tj., da se svjetlost prostire u kvantima koji
su nazvani fotoni. Više fotona izbacuje i više elektrona ali energija
izbačenih elektrona može da poraste samo ako poraste i energija fotona.
Ta Ajnštajnova pretpostavka bila je tada toliko radikalna da joj se suprotstavljao
i sam Plank, začetnik kvantne teorije.
Na osnovu svoje pretpostavke da fotoni predstavljaju kvante (čestice) svjetlosne energije, Ajnštajn je pokušao da objasni jedno eksperimentalno zapažanje Hajnriha Herca koji je eksperimentisao sa uglačanim metalnim kuglama kako bi proizveo radio-talase. U drugoj polovini XIX veka primjećeno je da, kada se metalna površina osvjetljava, dolazi do emisije elektrona sa nje (elektroni su nazvani fotoelektroni). Naučnici koji su se bavili ovim problemom su primjetili sledeće pojave:
- crvena svjetlost (velike talasne dužine) ne uspjeva da oslobodi elektrone, čak i kada je velikog intenziteta;
- s druge strane, ljubičasta svjetlost (male talasne dužine), čak i kada je srazmjerno slaba uspjeva vrlo lako da oslobodi elektrone;
- što je manja talasna dužina upadne svjetlosti, oslobođeni elektroni imaju veće kinetičke energije.
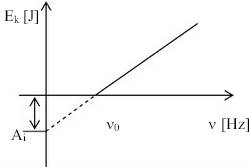 Sa
stanovišta klasične (talasne) teorije, rezultati su bili neobjašnjivi.
Prva i druga pojava ukazuju da postoji nekagranična frekvancija (tj. talasna
dužina) ispod koje se ne javlja fotoefekat. S obzirom da je u pitanju
crvena boja svjetlosti, granična vrijednost frekvencija je nazvana crvena
granica fotoefekta, ν0. Ona zavisi isključivo od osobina materijala. Ova
pojava je vidljiva i na grafiku zavisnosti kinetičke energijeoslobođenih
elektrona od frekvencije upadnog zračenja. Klasična (talasna) teorija
međutim kaže da bi fotoefekat morao da se pojavi na bilo kojoj frekvenciji,
pod uslovom da je intenzitet svjetlosti dovoljno veliki. S druge strane,
Ajnštajn je koristeći Plank-ovu jednačinu
zaključio dakada je talasna dužina svjetlosti mala, elektron prima dovoljno
energijeda se ″otrgne″ iz metala i poleti kroz vazduh. Znači, elektron
može ili da ″proguta″ cijeli foton ili ništa. Ako je energija koju sadrži
foton mala, elektron neće moći da pobjegne, bez obzira kolikim brojem
takvih fotona mi zasipali metal.
Sa
stanovišta klasične (talasne) teorije, rezultati su bili neobjašnjivi.
Prva i druga pojava ukazuju da postoji nekagranična frekvancija (tj. talasna
dužina) ispod koje se ne javlja fotoefekat. S obzirom da je u pitanju
crvena boja svjetlosti, granična vrijednost frekvencija je nazvana crvena
granica fotoefekta, ν0. Ona zavisi isključivo od osobina materijala. Ova
pojava je vidljiva i na grafiku zavisnosti kinetičke energijeoslobođenih
elektrona od frekvencije upadnog zračenja. Klasična (talasna) teorija
međutim kaže da bi fotoefekat morao da se pojavi na bilo kojoj frekvenciji,
pod uslovom da je intenzitet svjetlosti dovoljno veliki. S druge strane,
Ajnštajn je koristeći Plank-ovu jednačinu
zaključio dakada je talasna dužina svjetlosti mala, elektron prima dovoljno
energijeda se ″otrgne″ iz metala i poleti kroz vazduh. Znači, elektron
može ili da ″proguta″ cijeli foton ili ništa. Ako je energija koju sadrži
foton mala, elektron neće moći da pobjegne, bez obzira kolikim brojem
takvih fotona mi zasipali metal.
Istorijski razvoj
Herc je, 1887. godine primijetio da varnično pražnjenje između cinkanih kuglica postaje intenzivnije ukoliko se jedna od njih osvjetli ultraljubičastim zračenjem. Ispostavilo se da je suština ove pojave, nazvane fotoefektom, udaljavanje elektrona sa površine metala pod dejstvom UV zračenja. Detaljnu metodiku za ispitivanje ove pojave dao je ruski fizičar Stoletov. Njegova aparatura sastojala se od dve elektrode - katode, izgrađene od ispitivanog materijala, i anode, koje se nalaze u vakuumnoj cevi i priključene su na bateriju, tako da se potenciometrom može mijenjati ne samo vrijednost, nego i znak napona U, koji se dovodi. Kada se katoda osvjetli monohromatskom svjetlošću (kroz kvarcni prozor), sa nje se izbijaju elektroni, koji se, zatim, održavanjem napona ubrzavaju do anode. Javlja se fotoelektrična struja koja se mjeri miliampermetrom. Osvjetljavajući katodu svjetlošću različitih talasnih dužina (tj. različitih frekvencija), Stoletov je utvrdio sledeće zakonomernosti:
- Da najefektivnije delovanje ima UV zračenje;
- Da pod dejstvom svetlosti materijal gubi samo negativna naelektrisanja (1897. godine Tomson je izmjerio specifično negativno naelektrisanje, naelektrisanje čestice, koja je 1903. godine nazvana elektron);
- Da je jačina struje koja se javlja usled osvjetljavanja katode direktno proporcionalna intenzitetu upadne svjetlosti.
Karakteristike
Na osnovu izučavanja zavisnosti fotostruje I, obrazovane elektronima emitovanim sa katode pod dejstvom svetlosti, od napona U između elektroda, različitih materijala u vakuumu, za različite frekvencije upadnog zračenja, utvrđena su tri osnovna zakona spoljašnjeg fotoefekta:
- Stoletov zakon: pri fiksiranoj vrednosti frekvencije upadne svjetlosti, broj fotoelektrona, istrgnutih u jedinici vremena, proporcionalan je intenzitetu svjetlosti (jačina fotostruje zasićenja proporcionalna je energetskoj osvjetljenosti katode);
- Maksimalna početna brzina (maksimalna kinetička energija) fotoelektrona ne zavisi od intenziteta upadne svjetlosti, već je određena samo njenom frekvencijom;
- Za svaki materijal postoji crvena granica fotoefekta, tj. minimalna frekvencija svjetlosti (koja zavisi od hemijske prirode materijala i stanja njegove površine), ispod koje je fotoefekat nemoguć.
Problem sa tačke gledišta klasične elektrodinamike
Objašnjenje fotoefekta sa talasne tačke gledišta, na prvi pogled, ne bi trebalo da predstavlja poteškoće. Zaista, pod dejstvom polja svetlosnog talasa, u metalu se javljaju prinudne oscilacije elektrona, čije su amplitude (npr. pri rezonanci) dovoljno velike da elektroni napuste metal (tada se i primjećuje fotoefekat). Kinetička energija elektrona istrgnutog iz metala trebalo bi da zavisi od intenziteta upadne svjetlosti, jer bi sa povećanjem intenziteta upadne svjetlosti elektronu trebalo da se predaje više energije. Ali, ovaj zaključak protivrječi drugom zakonu fotoefekta. Naime, po talasnoj teoriji, energija, koja se predaje elektronima, proporcionalna je intenzitetu svjetlosti. Onda bi svjetlost bilo koje frekvencije, ali dovoljno velikog intenziteta, morala da otrgne elektrone iz metala; drugim riječima, crvena granica fotoefekta ne treba da postoji, što protivrječi trećem zakonu fotoefekta. Pored toga, talasna teorija nije mogla da objasni bezinertnost (trenutnu pojavu fotoefekta, tj. to što ne postoji mjerljivo vremensko kašnjenje od trenutka osvjetljavanja metala do detektovanja fotoelektrične struje) fotoefekta, utvrđenog eksperimentima. Na taj način, fotoefekat je neobjašnjiv sa tačke gledišta talasne teorije svetlosti.
Ovde je trebalo odlučno raskinuti sa starom teorijom, i tada je, u čuvenom radu iz 1905. godine, Ajnštajn, kao mladi činovnik instituta u Bernu, izložio vrlo smjelu hipotezu.
Ajnštajnova jednačina spoljašnjeg fotoefekta
 Ajnštajn
je pretpostavio da se svjetlosni talas sastoji od velikog broja kvanata
(koji su tek 1926. godine dobili ime fotoni). Saglasno Ajnštajnu,
svjetlost frekvencije ν ne samo da se ispušta u pojedinačnim porcijama
- kvantima, kako je to već ranije postavio Plank, već se i prostire
u prostranstvu i apsorbuje supstancom u pojedinačnim kvantima,
čija je energija E=hν. Na taj način prostiranje svjetlosti treba razmatrati
ne kao neprekidan talasni proces, nego kao protok lokalizovanih, u prostoru
diskretnih, svjetlosnih kvanata, koji se kreću brzinom prostiranja svjetlosti
u vakuumu.
Ajnštajn
je pretpostavio da se svjetlosni talas sastoji od velikog broja kvanata
(koji su tek 1926. godine dobili ime fotoni). Saglasno Ajnštajnu,
svjetlost frekvencije ν ne samo da se ispušta u pojedinačnim porcijama
- kvantima, kako je to već ranije postavio Plank, već se i prostire
u prostranstvu i apsorbuje supstancom u pojedinačnim kvantima,
čija je energija E=hν. Na taj način prostiranje svjetlosti treba razmatrati
ne kao neprekidan talasni proces, nego kao protok lokalizovanih, u prostoru
diskretnih, svjetlosnih kvanata, koji se kreću brzinom prostiranja svjetlosti
u vakuumu.
Energijski bilans pri fotoefektu može se izraziti kao:
![]()
gdje su:
![]() - jonizaciona energija potrebna da elektron napusti atom (za metale se ona može smatrati jednakom nuli, jer metal sadrži veliki broj slobodnih elektrona);
- jonizaciona energija potrebna da elektron napusti atom (za metale se ona može smatrati jednakom nuli, jer metal sadrži veliki broj slobodnih elektrona);
![]() - izlazni rad elektrona iz materijala, koji predstavlja minimalnu energiju koja je potrebna da bi elektron napustio površinu određenog materijala;
- izlazni rad elektrona iz materijala, koji predstavlja minimalnu energiju koja je potrebna da bi elektron napustio površinu određenog materijala;
![]() - kinetička energija fotoelektrona.
- kinetička energija fotoelektrona.
Za metale, prethodna jednačina ima oblik:
![]() .
.
Na osnovu prethodne relacije, minimalna vrijednost frekvencije ![]() upadnog ugla talsa, pri kojoj može doći do fotoefekta, iznosi:
upadnog ugla talsa, pri kojoj može doći do fotoefekta, iznosi:
![]() .
.
Minimalna talasna dužina svetlosti ![]() pri kojoj može doći do fotoefekta, je crvena granica.
pri kojoj može doći do fotoefekta, je crvena granica.
Objašnjenje fotoefekta je krajnje jednostavno: pri apsorpciji, foton predaje svu svoju energiju elektronu, trenutno, i ako je ova energija dovoljno velika da elektron raskine veze koje ga drže u metalu, on iz njega izleće. Kako je vjerovatnoća da jedan elektron primi energiju od dva fotona zanemarljivo mala, svaki oslobođeni elektron primio je energiju od samo jednog fotona. Zato broj oslobođenih elektrona treba da bude proporcionalan broju apsorbovanih fotona, odnosno proporcionalan intenzitetu upadnog talasa. Ali, kako energija elektrona koji izleće zavisi od energije samo jednog fotona (a svi fotoni su iste energije), slijedi da energija fotoelektrona treba da pokazuje linearnu zavisnost od frekvencije talasa, a da uopšte ne zavisi od intenziteta talasa.
Besprjekorna Ajnštajnova relacija za fotoefekat morala je da sačeka svoju potvrdu punih 11 godina, kada je Milikan, 1916. godine, uspeo da pomoću dosta komplikovane aparature potvrdi Ajnštajnovu hipotezu o kvantima svjetlosti, i da sa velikom tačnošću i on odredi Plankovu konstantu.
Tipovi
Danas se razlikuju tri vida fotoefekta: spoljašnji, unutrašnji i ventilni.
-
Spoljašnji fotoefekat
Spoljašnjim fotoefektom (koji se, takođe, naziva i samo fotoefekat) nazvana je pojava ispuštanja (udaljavanja) negativnog naelektrisanja (konkretno elektrona) sa površine materijala koji je izložen dejstvu elektromagnetskog zračenja. Spoljašnji fotoefekat primećuje se kod čvrstih tela (metala, poluprovodnika, dielektrika), a takođe i u gasovima na pojedinačnim atomima i molekulima (fotojonizacija).
-
Unutrašnji fotoefekat
Unutrašnji fotoefekat predstavlja pojavu da pod dejstvom elektromagnetskog zračenja dolazi do prelaska elektrona unutar poluprovodnika ili dielektrika, iz vezanih stanja u slobodna, bez njihovog izletanja van ovih materijala. Kao rezultat toga, koncentracija nosioca struje (elektrona) unutar materijala raste, što dovodi do pojave fotoprovodljivosti (povećanja elektroprovodnosti poluprovodnika ili dielektrika pri njihovom osvjetljavanju), tj. do pojave elektromotorne sile.
-
Ventilni fotoefekat
Ventilni fotoefekat je jedan oblik unutrašnjeg fotoefekta, tačnije pojava fotoelektromotorne sile pri osvjetljavanju kontakta dva različita materijala - dva različita poluprovodnika ili poluprovodnika i metala. Ventilni fotoefekat otvara puteve za direktno preobrazovanje sunčane energije u električnu.
Primjena fotoefekta
- spoljašnjeg: u vakuumnim fotoelementima i u fotomultiplikatorima;
- unutrašnjeg: u fotootpornicima ili u poluprovodničkim fotoelementima;
- ventilnog: u fotoelementima sa zakočnim slojem ili takozvanim ventilnim fotoelementima.
Važno je koliko energije ima u svakom fotonu ponaosob, a ne koliko fotona
ima, tj. koliki je intenzitetsvetlosti.Dalje: primećeno je (vidi se i
sa grafika) da maksimalna kinetička energija emitovanih elektrona linearno
raste sa povećanjem frekvencije upadnog zračenja i da uopšte ne zavisi
od intenziteta svetlosti. Prema klasičnoj teoriji, svetlostvećeg intenziteta
nosi sa sobom više energije pa bi sa povećanjem intenziteta morala da
raste i kinetička energijaelektrona. Međutim, prema Ajnštajnovoj hipotezi,
veći intenzitet znači samo veći broj fotona što može, ako im je energijadovoljna,
da proizvede većibrojoslobođenih elektrona, ali nema uticaja na njihovu
kinetičku energiju.
Povećanje intenziteta upadne svetlosti dovodi samo dopovećanja brojaoslobođenih
elektrona, ali nemauticaja na njihovu kinetičku energiju.I još jedna primećena
pojava: elektroni se sa površine metala emituju odmah (10-9s) posle osvetljavanja,čak
iako je intenzitet svetlosti mali. Prema klasičnoj teoriji se očekivalo
da elekton kumulativno apsorbuje energiju i da se osloboditek kada nakupi
dovoljno energije. Međutim, kao što je Ajnštajn rekao, elektron ili odmah″ proguta″foton
i oslobodi se ili se ne desi ništa (ako energija fotona nije dovoljno
velika). Znači, u pitanju je interakcija jedan-na-jedan; jedan foton i jedan
elektron. U toj interakciji foton se ponaša kao čestica.
Šta se u stvari dešava kada obasjamo površinu nekog metala elektromagnetnim
zračenjem? Kada padnena površinu metala, foton energije hν stupa
u interakciju sa postojećim elektronom. Ako je energija fotona dovoljnovelika
(ν >ν0– crvene granice), elektron će u potpunosti da apsorbuje
foton. Deo te energije elektron će da utorši da seoslobodi veza u metalu
i da izađe iz njega (tzv. izlazni rad metala koji se označava sa Ai),
a preostali deo energije setransformiše u kinetičku energiju elektrona.
S obzirom da kod metala elektroni napuštaju površinu metala, sam efekat
se naziva spoljašnji fotoefekat. Kod poluprovodnika i dielektrika,
elektroni i dalje ostaju u materijal, ali se znatno povećava provodnost
materijala. Taj efekatse naziva unutrašnji fotoefekat. Upadna svetlost
izaziva prelazak elektrona iz valentne u provodnu zonu, tj. izaziva fotojonizaciju.
Bez obzira koji tip fotoefekta je u pitanju, važno je da se naglasi da
se za vreme interakcije sa elektronom foton PONAŠA KAO ČESTICA. Znači,
elektromagnetni talasi imaju dvostruku, dualnu prirodu, neki put se ponašaju
kaotalasi, a neki put kao čestice. Fotofekat ima veoma široku primenu.
Praktično svi optički senzori u svojoj osnovi imaju fotoefekat. Raznidetektori,
fotodiode, fototranzistori, pačak i solarnećelije se zasnivaju na pojavi
oslobađanja elektrona (ilipovećanja izlazne struje) pod dejstvom svetlosti.
- S. Macura, J. Radić-Perić, ATOMISTIKA, Fakultet za fizičku hemiju Univerziteta u Beogradu/Službeni list, Beograd, 2004, str. 231.
- www.wikipedia.com
- www.scribd.com
preuzmi
seminarski rad u wordu » » »
