Познато је да се многе области математике ослањају, користе знања и преплићу са другим математичким дисциплинама. Тако теореме о „непокретној тачки“ имају врло значајне примена у различитим математичким дисциплинама. Поменимо, на пример, Банахову теорему о непокретној тачки за контракције на метричким просторима која има значајну примерну у доказивању егзистенције и јединствености решења обичних диференцијалних једначина. У овом раду биће речи о, не мање познатој Брауеровој теореми о непкретној тачки.
Најједноставнији случај те теореме предстваља следеће тврђење: дат је интервал [a,b] и непрекидна функција f : [a,b] → [a,b]. Тада функција f има барем једну непокретну тачку.
Да бисмо то доказали направимо нову (помоћну) функцију Φ дефинисану на следећи начин Φ(x) = f(x) - x. Очигледно важи f(a) ≥ a и f(b) ≤ b, односно

Φ(а) = f(a) - a ≥ 0,

Φ(b) =f(b) - b ≤ 0.

Тада, према Болцановој теореми постоји тачка x* таква да је Φ(x*) = 0, односно f(x*) = x*, чиме је тврђење доказано.
Изнећемо доказ одговарајућег тврђења за диск у равни, као и скицу како се то тврђење може пренети и у више димензије.

2. Непрекидна пресликавања и хомеоморфизам

Нека су X и Y подскупови метричког простора Rn. Кажемо да су скупови X и Y хомеоморфни ако постоји бијекција h : X → Y, таква да су оба пресликавања h и h-1 непрекидна. Такво пресликавање h зовемо хомеоморфизам.
За скуп X кажемо да има својство непокретне тачке, ако свако непрекидно пресликавање f : X → X има барем једну непокретну тачку. На пример, према ономе што смо изложили у уводу интервал [a,b] има својство непокретне тачке.
Својство непокретне тачке се преноси са скупа X на било који њему хомеоморфан скуп. Заиста, нека X има својство непокретне тачке, нека је h : X → Y хомеоморфизам и нека је f : Y → Y произвољно непрекидно пресликавање. Тада је h-1◦f◦h : X → X непрекидно пресликавање и има барем једну непокретну тачку x. То значи h-1(f(h(x))) = x, односно f(h(x)) =h(x), па је y = h(x) непокретна тачка пресликавања f.

3. Брауерова теорема у равни

У овом одељку доказаћемо једно уопштење тврђења из увода. Наиме, уместо интервала посматраћемо диск у равни.
Дакле, нека је дат кружни диск у равни, односно област која се састоји из унутрашњости круга заједно са рубом. На тај диск, односно на његове тачке, деловаће нека непрекидна трансформација која не мора бити бијекција, али тако да при тој трансформацији све тачке диска остају унутар њега, другачије распоређене.
Као пример нам може послужити танак гумени диск, а трансформација о којој је било речи може бити свака његова деформација при којој ће све тачке почетног диска остати унутар новодобијеног лика. Значи, тај гумени диск можемо савити, увити, гужвати, растегнути и слично. Или, као још један пример, узмимо чашу воде а кашичицом ћемо мешати садржину чаше, али тако да честице са површине, по завршетку мешања, и остану на површини, али на неком другом месту.
Брауерова теорема каже следеће: свака оваква трансформација оставља бар једну тачку непокретном, то јест постоји макар једна тачка чији ће положај након трансформације остати непромењен.
Да бисмо ово доказали, претпоставићемо супротно – ниједна тачка после трансформације није остала у истом положају, већ је свака тачка постала нека друга.

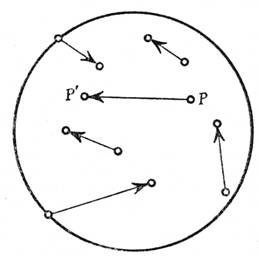Свакој тачки P из полазног диска припишимо вектор PP’, где је P’ слика тачке P при датој трансформацији. Свакој тачки приписан је тачно један вектор. Поставља се питање шта је са тачкама са руба? Пошто смо тако дефинисали трансформацију, тачке са руба диска ће се сликати у његову унутрашњост. Уочимо неку тачку P1 са руба, која путује по кругу у правцу супротном сказаљки на сату. Правац вектора ће се мењати, јер тачке на рубу имају приписане векторе који су различито управљени. На путу по кругу од P1 до P1 вектор се окреће и враћа у почетни положај. Број потпуних обртаја који је вектор учинио назовимо „индексом“ вектора на кругу. То је збир разних промена у углу вектора, тако да обртај у правцу сказаљке на сату узимамо као негативан, док ћемо обртај у правцу казаљке на сату узети за позитиван. Значи, индекс може бити 0, ±1, ±2, ±3,…, а биће остварен при укупној промени угла за 0, ±360, ±720, ±1080,... степени.
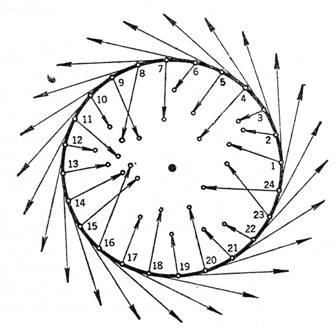Brauerova teorema o nepokretnoj tacki

Сада тврдимо да је индекс једнак тачно један, то јест да вектор један пун круг у смеру супротном сказаљки на сату. Сетимо се да је вектор сваке тачке са руба усмерен ка унутрашњости диска а не по тангенти. Ако се вектор трансформације обрне за укупан угао који се разликује од укупног угла за који се окреће тангентни вектор (који је 360 степени, јер тaнгентни вектор чини један комплетан позитивни обртај), разлика између укупних углова кроз који се тангентни и трансформациони вектор окрену је неки не-нула множилац од 360 степени, јер сваки чини један цео број обртаја. Дакле, вектор трансформације мора се потпуно окренути бар један пут за време кружења од P1 до P1. Тангентни и трансформациони вектор се непрекидно крећу, па ће у некој тачки на кругу трансформациони вектор бити усмерен у правцу тангенте, а ово није могуће.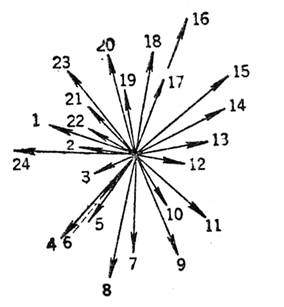

Уочимо неки круг који је концентричан са рубом диска и садржан је у њему, заједно са одговарајућим трансформационим векторима на том кругу. Тада индекс трансформационих вектора на њему мора такође бити један. Ако се непрекидно крећемо од тачке руба до било ког концентричног круга, индекс се непрестано мења, али он мора бити целобројна вредност, па мора бити стално једнак својој почетној вредности један, јер би скок са један на неки други цео број био прекид у понашању индекса. Према томе, уочићемо концентричан круг који је произвољно мали, за који је индекс вектора трансформације једнак један. Ово није могуће јер смо претпоставили непрекидност трансформације, па ће вектори на довољно малом кругу бити апроксимативно усмерени у истом правцу као и вектор у центру круга. Дакле, укупна промена углова може бити произвољно мала, на пример мања од 10 степени за довољно мали круг. Како индекс мора бити цео број – биће нула. Дошли смо до контрадикције, што значи да претпоставка о непостојању непокретне тачке није тачна, чиме је теорема доказана.
Доказана теорема важи како за диск, тако и за троугласту или квадратну површ, или неку другу диску хомеоморфну површ, што видимо на основу разматрања из другог одељка.

4. Брауерова теорема у више димензија

Доказ изложен у претходном одељку (видети [1]) не можемо пренети на димензију 3 или више. Међутим, Брауерова теорема важи и за тродимензионе објекте као што су лопта, коцка или неко њима хомеоморфно тело, и за одговарајуће подскупове простора Rn.
Друкчији доказ који важи у свим димензијама дат је у [2], али његово излагање захтева детаљније проучавање топологије.
Уместо доказа за димензије веће од три, изложићемо како се Брауерова торема може свести на једно друго тврђење које је очигледније.
Нека је . Пресликавање f : A → B називамо ретракција, ако је непрекидно и ако је ѕа све x из B f(x) = x.
Illustration of the retraction F Нека је Bn јединична лопта у Rn. Тада не постоји ретракција са Bn на његов руб. Ово тврђење нећемо доказивати, али рачунамо да је интуитивно јасно. Наиме, у случају да таква ретракција постоји, унутрашњост лопте би се негде морала прекинути.
Излажемо скицу доказа Брауерове теореме у више димензија:
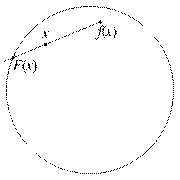
Претпоставимо супротно да непрекидна функција f : Bn → Bn нема непокретну тачку. Тада за све x из Bn постоји јединствена полуправа са почетком у f(x) која пролази кроз x. Њен пресек са рубом лопте означимо са F(x) (слика). Тиме добијамо непрекидно пресликавање F: Bn → ∂Bn, такво да за све x из ∂Bn важи F(x) = x.

5. Историјат

Брауерова теорема о непокретној тачки, једна је од првих достигнућа алегбарске топологије, и чини основу за општије теореме о непокретној тачки важне у функционалној анализи. Случај n = 3, први је доказао Piers Bohl 1904 године (објављено у Journal für die reine und angewandte Mathematik). Касније је доказао холандски математичар L. E. J. Brouwer 1909, по коме и носи име. Жак Адамар (Jacques Hadamard) је доказао општи случај 1910, а Брауер је дао друкчији доказ 1912. Ови први докази нису имали конструктивни карактер већ су били индиректни, базирали су се на оповргавању супротне претпоставке, супротно Брауеровим интуиционистичким идеалима. Данас су познати методи за приближно одређивање непокретне тачке, чије постојање гарантује Брауерова Теорема (Karamadian 1977) и (Istrăţescu 1981).

Литература

[1] R. Courant, H. Robbins „Šta je matematika?“, Naučna knjiga, Beograd, 1973
[2] M. Marjanović, Topologija, Matematički Fakultet, Beograd, 1990
[3] http://en.wikipedia.org/wiki/Brouwer_fixed_point_theorem

PROČITAJ / PREUZMI I DRUGE SEMINARSKE RADOVE IZ OBLASTI:

preuzmi seminarski rad u wordu » » »

Besplatni Seminarski Radovi