Broj Φ i Fibonačijev niz

Zlatni presek  u elementarnoj geometriji.

Zlatni presek je proporcija koja se često spominje kada se razmatraju odnosi rastojanja kod jednostavnih geometrijskih figura. Euklid postavlja u jedanaestom stavu druge knjige svojih Elemenata sledeći zadatak:

˝Datu duž podeli tako da pravougaonik obuhvaćen celom duži i jednim odsečkom bude jednak kvadratu na drugom odsečku.˝

Iz konstrukcije gornjeg zadatka sledi podela date duži po zlatnom preseku, iako Euklid izričito napominje da se manji deo duži (minor), odnosi prema većem (major) kao ovaj prema zbiru manjeg i većeg. Ovaj odnos Euklid naziva neprekidnom podelom ili podelom u srednjoj i krajnjoj razmeri.
Neka datu duž AB podelimo na dva dela tačkom T, tako da je:

AB:AT=AT:BT

Tada kažemo da oni čine zlatni presek. Kako konstruisati tačku koja datu duž deli tako da je odnos većeg dela prema manjem isti kao i odnos cele duži prema većem delu? Heron je to uradio na sledeći način:
Konstruišimo datu duž AB, zatim konstruišimo krug k koji dodiruje pravu AB u tački B, čiji je prečnik podudaran duži AB. Označimo sa C centar ovog kruga. Označimo tačku preseka duži AC i kruga k sa D. Zatim se konstrukcijom preseka kruga, čiji je centar u tački A i poluprečnik mu je AD, i duži AB dobija tačka T.

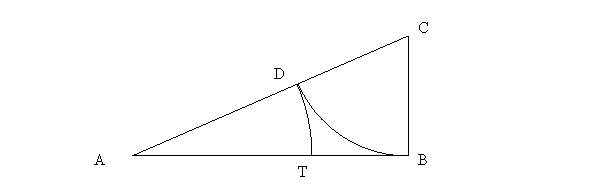
Ako su D i E tačke u kojima AC seče krug k, pri čemu je AD=AT, na osnovu teoreme o potenciji tačke u odnosu na krug biće

AB²=AD*AE
Pa je
AB*(AT+TB)=AD*(AD+AB)=AT*(AT+AB)
AB*AT + AB*TB=AT² + AT*AB
A odavde sledi da je:

AB*BT=AT²

Dakle, razlaganje duži AB tačkom T je zlatni presek.
Ako duž AB označimo sa a, a AT sa x, dobićemo relaciju:

a:x=x:(a-x)

a/x=x/(a-x)

Posmatrajući sliku, možemo zaključiti da je, na osnovu Pitagorine teoreme:

AC²=AB²+BC²
AC²=a²+(a/2)²
AC²=(5a²)/4
AC=√5*a/2

Takođe važi da je:
AC=a/2+x

Pa sledi da je:
√5*a/2=a/2+x
x=√5*a/2-a/2

x=a*(√5-1)/2

Pa je traženi odnos brojeva a:x jednak:

x/a=(√5-1)/2 tj. a/x=(√5+1)/2

Broj a/x nastao iz zlatnog preseka duži AB, koji nije racionalan jer √5 nije racionalan, se obično obeležava grčkim slovom Φ ili Phi. Mi ćemo ga obeležavati sa τ, kao prvo slovo reči τομή (presek). On iznosi:

τ=a/x=(√5+1)/2=1,6180339887...

Takođe možemo primetiti da je:

1/τ=x/a=(√5-1)/2=τ-1=0,6180339887...

odnosno da je 1+1/τ=τ. Možemo primetiti da je τ jedinstven realan broj kojem je recipročna vrednost za jedan manja od tog broja. Iz ove jednačine sledi da je τ koren kvadratne jednačine:
a²-a-1=0

Primenom ove nove oznake biće u znatnoj meri olakšano rukovanje neprekidnom podelom i omogućena bolja preglednost pojedinih brojeva ovog proporcijskog sistema.

Fibonačijevi brojevi

Početkom XIII veka Leonardo Fibonacci (1180-1240) je upoznao Evropu sa radovima indijsko-arapskih matematičara, a time neposredno i kineskih. On je u svojoj raspravi Liber abaci (˝knjiga o abaku˝) 1202. godine izložio praktičan aritmetički problem:

˝Koliko pari zečeva će reprodukovati jedan par za godinu dana ako se pretpostavi da svakog meseca jedan par rodi novi par koji za dva meseca postane reproduktivan?˝

Zanimljiv je redosled brojeva do kojeg je došao proučavajući razmnožavanje zečeva. Rešavanjem ovog zadatka dobio je niz brojeva na sledeći način: prvog meseca eksperiment počinje jednim parom zečeva, u drugom mesecu će postojati samo taj jedan par, u trećem mesecu će ih biti 2, u četvrtom 3, u petom 5, u šestom 8 itd.
Ovom nizu brojeva je francuski matematičar Edvard Lucas (1842-1891) dao ime Fifonaccijevi brojevi i otkrio njihove važne primene.
Fibonaccijevi brojevi ili, kako ih često nazivamo, Fibonaccijev niz je vrsta rekurzivnog niza u kojem zbir dva prethodna člana daje sledeći broj.

 Fibonaccijevi brojevi su najjednostavnija vrsta rekurzivnog niza. U ovom rekurzivnom nizu za formiranje n-tog člana reda moramo znati dva člana koji mu prethode. Dakle, za poznavanje ovog niza su najvažnija prva dva člana F1 i F2, jer se ostali članovi mogu dobiti iz relecije:

Fn=Fn-1+Fn-2

Fibonači je otkrio neobične osobine ovog niza.
Deleći svaki broj u Fibonačijevim nizu sa onim koji mu prethodi, dolazimo do sledećeg brojnog odnosa:

1/1 =1
2/1 =2
3/2 =1,5
5/3 =1,66...
8/5 =1,6
13/8 =1,625
21/13 =1,615384
34/21 =1,619047
55/34 =1,617647
89/55 =1,618181
....

Kepler je utvrdio da je odnos dvaju susednih članova niza u beskonačnosti teže vrednosti zlatnog preseka. Dokazano je ponavljanjem relacije:
1+1/τ=τ
na sledeći način:
1+1/(1+1/τ)= 1+1/(1+1/(1+1/τ))=...

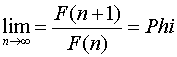
Postoji interesantan niz jednačina za Fibonačijeve brojeve:

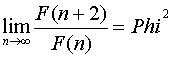
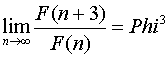
U opštem slučaju imamo:

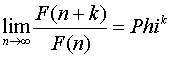
Imamo sledeće relacije između Fibonačijevih brojeva i zlatnog preseka:

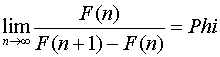
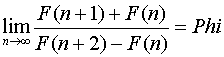
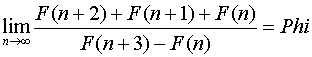
Ili u opštem slučaju:

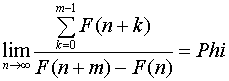
Pascalov trougao

Numeričke trouglove čine nizovi brojeva sa nekom pravilnošću. Posmatrajmo sledeći trougaoni raspored brojeva:

Ovakav trougao je dobio naziv Paskalov trougao, po francuskom matematičaru Blaise Pascalu (1623-1662). Otac nije dozvolio mladom Blaiseu da uči matematiku sve dok ne napuni 15 godina, pa je matematičke knjige uklonio iz kuće. Znatiželja izazvana tim činom navela je Paskala da od 12 godina počne da samostalno proučava geometriju. Nedugo zatim otkrio je da zbir uglova u trouglu iznosi dva prava ugla. Kada je njegov otac doznao za sinovo otkriće, dozvolio mu je da proučava Euklidovu geometriju. Već sa 16 godina predstavlja nekoliko svojih radova iz oblasti projektivne geometrije.
Po nekim dokazima arapski astronom, pesnik i matematičar Omar Hajam je poznavao ovaj brojni trougaoni raspored još u XI veku. Najverovatnje je ovaj brojni trougao krenuo iz Kine preko Arapskog sveta u Evropu. Kineski prikaz binomnih koeficijenata, koji često nazivaju i Paskalovim trouglom, jer ga nalazimo u istoimenom Paskalovom delu u vezi sa figurativnim brojevima, zabeležen je prvi put na naslovnoj strani Evropske aritmetike od Apianusa. Taj trougao je krajem XVII veka postao središnja tačka razvoja tri grane matematike: proučavanja beskonačnih redova, računa konačnih diferencija i teorije verovatnoće.
Paskalov trougao je povezan sa Fibonačijevim brojevima, a veliku ulogu ima i u određivanju binomnih koeficijenata u razvoju binoma. Direktnim množenjem se može lako proveriti tačnost sledećih binomnih razvoja:

(a+b)0 =1
(a+b)1 =1*a + 1*b
(a+b)2 =1*a² + 2*ab + 1*b²
(a+b)3 =1*a³ + 3*a²b + 3*ab² + 1*b³
(a+b)4 =1*a4 + 4*a³b + 6*a²b² + 4*ab³ + b4
...

Binomni koeficijenti u binomnom razvoju čine Paskalov trougao.
Prometimo da je zbir članova svakog reda aritmetičkog trougla zapravo neki stepen broja dva.
Prva kolona aritmetičkog trougla je kolona jedinica. Figurativno jedinica predstavlja tačku. Posmatrajmo trougao čije su sve kolone nizovi jedinica.

1 1 =2
1 1 1 =3
1 1 1 1 =4
1 1 1 1 1 =5
1 1 1 1 1 1 =6
1 1 1 1 1 1 1 =7
.....

Sumiranje po osnovama ovog trougla daje drugu kolonu aritmetičkog trougla tj. kolonu prirodnih brojeva:1, 2, 3, 4, 5, 6, ... Niz prirodnih brojeva je figurativno prava linija. Sada posmatrajmo trougaonu tabelu čije su sve kolone upravo ovaj niz prirodnih brojeva:

1 =1
2 1 =3
3 2 1 =6
4 3 2 1 =10
5 4 3 2 1 =15
6 5 4 3 2 1 =21
7 6 5 4 3 2 1 =28
....

Primetimo da sumiranje po osnovama daje treću kolonu aritmetičkog trougla, kolonu takozvanih trougaonih brojeva: 1, 3, 6, 10, 15, 21, 28,... Razlika između svakog prethodnog broja je za jedan manja od sledećeg. Tako je između broja jedan i tri razlika dva, već između brojeva tri i šest razlika je tri.Trougaoni brojevi su simbol trougla i površine. Trougao u ravni čije su sve kolone nizovi trougaonih brojeva je dat u sledećoj formi:

 1 =1
3 1 =4
6 3 1 =10
10 6 3 1 =20
15 10 6 3 1 =35
21 15 10 6 3 1 =56 
28 21 15 10 6 3 1 =84
.....

Ovoga puta sumiranje brojeva po osnovama gornjeg trougla rezultuje tetraedarskim brojevima četvrte kolone aritmetičkog trougla. Niz ovih brojeva figurativno predstavlja tetraedre-piramide, a dimenziono zapreminu: 1, 4, 10, 20, 35, 56, 84,... Isti postupak se može primeniti i na ostale brojne kolone aritmetičkog trougla. Na taj način se gradi n-dimenzioni prostor a integracija je veza između susednih kolona aritmetičkog trougla.
Sumirajući brojeve na dijagonali Paskalovog trougla mogu se dobiti Fibonačijevi bojevi:

 1 =1
1 1 =1
1 2 1 =2
1 3 3 1 =3
1 4 6 4 1 =5
1 5 10 10 5 1 =8
1 6 15 20 15 6 1 =13
1 7 21 35 35 21 7 1 =21
.......

Ako napišemo dupli Paskalov trougao i sumiramo delove:

1 =1
1 1 =2
1 1 1 =3
1 1 2 1 =5
1 1 3 2 1 =8
1 1 4 3 3 1 =13
1 1 5 4 6 3 1 =21
.....

Igrajući se brojevima i prostorom ponovo ćemo ukazati na vezu aritmetičkog trougla i Fibonačijevih brojeva. Prikazaćemo Paskalov trougao u sledećoj varijanti i sabraćemo brojeve po osnovama:

1 =1
1 =1
1 1 =2
1 2 =3
1 3 1 =5
1 4 3 =8
1 5 6 1 =13
....

Sumirajući osnove Paskalovog trougla takođe se dobijaju Fibonačijvi brojevi.
Postoji obratna veza Fibonačijevih brojeva i aritmetičkog trougla. Ima mnoštvo rekurzionih formula za Fibonačijeve brojeve:

Fn+1=1*Fn + 1*Fn-1
Fn+2=1*Fn + 2*Fn-1 + 1*Fn-2
Fn+3=1*Fn + 3*Fn-1 + 3*Fn-2 + 1*Fn-3
Fn+4=1*Fn + 4*Fn-1 + 6*Fn-2 + 4*Fn-3 + 1*Fn-4
Fn+5=1*Fn + 5*Fn-1 + 10*Fn-2 + 10*Fn-3 + 5*Fn-4 + 1*Fn-5
......
Kako preko numeričkog trougla prikazati kvadrate svih prirodnih brojeva? Posmatrajmo sledeći trougao:

1
1 2 1
1 2 3 2 1
1 2 3 4 3 2 1
1 2 3 4 5 4 3 2 1
1 2 3 4 5 6 5 4 3 2 1
1 2 3 4 5 6 7 6 5 4 3 2 1
...

Zbir članova svakog reda daje rezultate: 1, 4, 9, 16, 25, 36, 49,... koji su kvadrati brojeva:1, 2, 3, 4, 5, 6, 7,...
Vidimo da je u ove rekurzione relecije za Fibonačijeve brojeve ugrađena struktura Paskalovog brojnog trougla, što nedvosmisleno ukazuje na vezu koja postoji između brojeva Paskalovog trougla i niza Fibonačijevih brojeva.

Lukasovi brojevi

Francuski matematičar Fransis Eduard Anatol Lucas (1842-1891) je proučavao Fibonačijevu seriju brojeva, i njoj pridružio jedan drugi niz koji je dobio naziv po njemu. Lucas je najpoznatiji po svojim rezultatima u oblasti teorije brojeva. Dokazao je da je broj 2127-1 prost broj. Osim u oblasti teorije brojeva Lukas je poznat i u zabavnoj matematici po svom problemu Hanojska Kula. Slikovitom kombinacijom Fibonačijevih brojeva mogu se dobiti takozvani Lukasovi brojevi. Preciznije, svaki Lukasov broj je zbir prethodna dva Lukasova broja. Razlika u definiciji je što Lukasov niz počinje sa 2 i 1 umesto sa 0 i 1.
Lukasovi brojevi su dati rekurzionom relecijom:

Ln+1=Ln-1+Ln, pod uslovom da je n>1 i L0=2, L1=1

Lukasov niz izgleda ovako:

1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, 322, 521, 843, ...

i njegovi članovi se dobijaju kao zbir određenih članova Fibonačijevog niza.

 1 2 3 5 8 13 21 34 55... 
 1 1 2 3 5 8 13 21...  +
1 3 4 7 11 18 29 47 76...

odnosno

Ln=Fn-1+Fn+1

Ovaj niz ima osobinu sličnu osobinama Fibonačijevog niza. Svaki novi član Lukasovog niza brojeva jednak je zbiru dva prethodna člana. Takođe, količnik dva uzastopna Lukasova broja teži vrednosti zlatnog preseka:

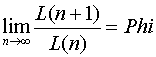
Postoji recipročna veza između Lukasovih brojeva i koeficijenata Paskalovog trougla. Postoji beskonačno mnogo rekurzionih relacija za Lukasove brojeve:

Ln+1 = 1*Ln + 1*Ln-1
Ln+2 = 1*Ln + 2*Ln-1 + 1*Ln-2
Ln+3 = 1*Ln + 3*Ln-1 + 3*Ln-2 + 1*Ln-3
Ln+4 = 1*Ln + 4*Ln-1 + 6*Ln-2 + 4*Ln-3 + 1*Ln-4
Ln+5 = 1*Ln + 5*Ln-1 + 10*Ln-2 + 10Ln-3 + 5*Ln-4 + 1*Ln-5
... ... ... ... ... ... ...

Očigledno je da je struktura Paskalovog trougla ugrađena u ove rekurzione relacije, koje sasvim pouzdano ukazuju na postojanje veze između koeficijenata Paskalovog trougla i Lukasovih brojeva.

Veza između Fibonačijevog i Lukasovog niza

Lukasovi brojevi se mogu na jednostavan način dobiti pomoću Fibonačijevih brojeva:

L(n) = 2F(n-1) + F(n)

I Fibočijevi brojevi se mogu izraziti preko Lukasovih brojeva. Na primer:

5*Fn+2 = 1*Ln + 3*Ln+1
5*Fn+3 = 3*Ln + 4*Ln+1
5*Fn+4 = 4*Ln + 7*Ln+1
5*Fn+5 = 7*Ln + 11*Ln+1
5*Fn+6 = 11*Ln + 18*Ln+1
... ... ...
5*Fn+k = Lk-1*Ln + Lk*Ln+1

Takođe je moguće i Lukasove brojeve izraziti pomoću Fibonačijevih brojeva, što ukazuje na njihovu međusobnu povezanost. Postoji beskonačna serija rekurzionih relacija za izračunavanje Lukasovih brojeva pomoću Fibonačijevih brojeva. Koeficijenti u ovim jednačinama grade niz Lukasovih brojeva:

Ln+2 = 1*Fn + 3*Fn+1
Ln+3 = 3*Fn + 4*Fn+1
Ln+4 = 4*Fn + 7*Fn+1
Ln+5 = 7*Fn + 11*Fn+1
Ln+6 = 11*Fn + 18*Fn+1
... ... ...
Ln+k = Lk-1*Fn + Lk*Fn+1

Veza između Lukasovih i Fibonačijevih brojeva je mnogostruka. Prethodnim rekurzionim jednačinama simetrične su neke druge grupe jednačina. Na primer, rekurzione jednačine koje služe za izračunavanje Lukasovih brojeva sa Fibonačijevim brojevima kao koeficijentima.

Ln+2 = 1*Ln + 1*Ln+1
Ln+3 = 1*Ln + 2*Ln+1
Ln+4 = 2*Ln + 3*Ln+1
Ln+5 = 3*Ln + 5*Ln+1
Ln+6 = 5*Ln + 8*Ln+1
... ... ...
Ln+k = Fk-1*Ln + Fk*Ln+1

Takođe se mogu napisati rekurzione jednačine za izražavanje Fibonačijevih brojeva preko Fibonačijevih brojeva.

Fn+2 = 1*Fn + 1*Fn+1
Fn+3 = 1*Fn + 2*Fn+1
Fn+4 = 2*Fn + 3*Fn+1
Fn+5 = 3*Fn + 5*Fn+1
Fn+6 = 5*Fn + 8*Fn+1
... ... ...
Fn+k = Fk-1*Fn + Fk*Fn+1

Obrazujmo niz od zbira četri uzastopna Lukasova broja tj.

Ln+Ln+1+Ln+2+Ln+3
(1+3+4+7), (3+4+7+11), (4+7+11+18), (7+11+18+29),...

Tada dobijamo Fibonačijev niz brojeva 5*Fn+3, odnosno:

5*(3, 5, 8, 13, 21,...)

Kao što znamo, broj τ je koren kvadratne jednačine:

a² – a – 1 =0

Takođe važi jednačina 1 + 1/τ = τ . Označimo broj 1/ τ sa T, i tada zamenjujući u kvadratnu jednačinu dobijamo:

(1+T)²–(1+T)–1=0
1+2T+T²-1-T-1=0
T²+T-1=0

Znači, 1/τ je koren prethodno dobijene kvadratne jednačine.
Postoje iznenađujuće veze između zlatnog preseka i Fibonačijevih i Lukasovih brojeva. U formulama za Fibonačijeve brojeve koristimo operatorsku jednačinu:

H²+H=1

koji je analogna sa dobro poznatom jednačinom:

T²+T=1

što će značiti da je 
T≡H

Za Fibonačijeve i Lukasove brojeve koristimo sledeće operatorske jednačine:

H=1/(1+H)
1+H=1/H

Koristeći dve jednačine možemo napisati:

1+H=1+1/(1+H)=(2+H)/(1+H)

Tada dobijamo sledeći niz jednačina:

1 = 2*H² + 1*H³
1 = 3*H³ + 2*H4
1 = 5*H4 + 3*H5
1 = 8*H5 + 5*H6
1 = 13*H6 + 8*H7
...
ili u opštem slučaju:

1 = Fn+1*Hn + Fn*Hn+1

Koristeći identitet između H i T možemo pisati:

1 = Fn+1*Hn + Fn*Hn+1
(1/T)n = Fn+1 + Fn*T

Za Lukasove brojeve dobijamo sledeću jednakost:

Ln+1 = Tn + (1+T²)*Fn

Binetova formula za dobijanje Fibonačijevih brojeva

Binetova formula za n-ti član Fibonačijevog niza dobija se rešavanjem rekurentnih jednačina.

α+β=1  ۷ α*β=-1
an+1=( α+β) an - α*β an-1
an+1- αan= β(an-α an-1)

Pa, dobijamo niz jednakosti:

an+1- αan= β(an-α an-1)
= β²(an-1-α an-2)
= β3(an-2-α an-3)
...
= βn-2(a3-α a2)
= βn-1(1-α)

Ako svaku od poslednjih jednakosti izjednačimo sa poslednjom, dobijamo:

an- αan-1= βn-2(1-α)
an-1- αan-2= βn-3(1-α)
an-2- αan-3= βn-4(1-α)
...
a3- αa2= β(1-α)
a2- αa1= β0(1-α)

Ako pomnožimo prvu jednakost sa α0, a drugu sa α2, treću sa α0, pretposlednju sa αn-3, a poslednju sa αn-2, dobićemo:

an- αan-1= βn-2(1-α)
αan- α2an-1=αβn-3(1-α)
α2an-2- α3an-3= α2βn-4(1-α)
....
αn-3a3- αn-2a2= αn-3β(1-α)
αn-2a2- αn-1a1= αn-2β0(1-α)

Saberimo sada ove jednakosti:

an- αn-1=(1-α)( α0βn-2 + αβn-3 +...+ αn-3β + αn-2β0)
an- αn-1=(1-α)( αn-1- βn-1)/( α- β)

an=( αn- βn)/( α- β)

Ako se vratimo na početak i prisetimo se da smo α i β birali kao rešenja jednačine

t²-t-1=0

α=(1+√5)/2 β=(1-√5)/2

an=[ ( (1+√5)/2)n-( (1-√5)/2)n ] / √5
Pa dobijamo:

Fn= ((1+√5)n-(1-√5)n)/ 2n√5

Sabiranje, oduzimanje i množenje m-tog i n-tog člana Fibonačijevog niza

Ako je poznat 3. i 5. član, koju vrednost ima 8. član Fibonačijevog niza? Kako je indeks traženog člana mali broj, njegovu vrednost lako možemo izračunati. Međutim, kada su u pitanju brojevi koji se ne nalaze na samom početku niza, situacija postaje malo složenija.
Neka su dati m-ti i n-ti član niza. Broj koji je na n+m-toj poziciji Fibonačijevog niza određujemo na sledeći način:

Fn+m=( FnLm+FmLn )/2

Ako su nam poznati n-ti i m-ti članovi, a hoćemo da znamo m-n-ti, odredićemo ga pomoću formule:

Fm-n=(-1)n( FmLn-FnLm )/2

Ako želimo da pod istim uslovima znamo m*n-ti član Fibonačijevog niza, možemo koristiti sledeću formulu:

Fmn=L(m)Fm(n-1) - (-1)mFm(n-2)

Neki algebarski identiteti Fibonačijevog niza

Kako ćemo sada na osnovu prethodnih formula odrediti 2n-ti član kada nam je poznat n-ti?

F2n=Fn+n
=(FnLn+FnLn)/2
=FnLn
=Fn(Fn-1+Fn+1)
=(Fn+1-Fn-1) * (Fn-1+Fn+1)
=F²n+1- F²n-1
tj.

F2n= Fn(Fn-1+Fn+1)

Na sličan način dobijamo da je:

F3n=F³n+1-F³n+F³n-1

Takođe važe i sledeći identiteti:

F²n+1=4FnFn-1+ F²n-2

Suma svih brojeva do nekog n-tog člana se može izračunati po formuli:

F1+F2+F3+...+Fn=Fn+2-1

Dokažimo da se suma kvadrata prvih n članova Fibonačijevog niza računa po formuli:

F²1+F²2+F²3+...+F²n=FnFn+1

Koristeći matematičku indukciju, ispitujmo prvo da li je jednakost tačna za n=1.

F²1=F1*F1+1
F²1=F1*F2
1²=1*1

Jedankost je tačna. Pretpostavimo da je jednakost ispunjena za n. Proverićemo da li tvrđenje važi i za n+1. član.

F²1+ F²2+ F²3+...+ F²n+ F²n+1= F²n+1+FnFn+1
=Fn+1*(Fn+1+Fn)
=Fn+1*Fn+2
Time smo dokazali dati identitet.
Poznati su nam još neki identiteti, kao što su:

Honsbergove relacije Fn+m=Fn-1Fm+FnFm+1
F(k+1)n=Fn-1Fkn+FnFkn+1
Fn=F2(n+1)/2+ F²(n-1)/2

D'Ocanenov identitet F4n-Fn-2Fn-1Fn+1Fn+2=1

Catalanijev identitet F2n-Fn+rFn-r=(-1)n-rF²r

Cassinijev identitet Fn+1Fn-1- F2n=(-1)n

Kvadratni izraz F2n=(L2n-2(-1)n)/5
Fn+1=(Fn+Ln)/2

Zanimljiva svojstva broja τ

Kao što znamo, τ je koren kvadratne jednačine a²-a-1=0, pa važi jednačina:

τ²-τ-1=0

Pa, možemo zaključiti da je kvadrat boja τ jednak broju τ uvećanom za jedan. Ovaj izraz možemo svesti na kvadrat binoma, tako što, kao prvo, rastavimo zadnji član.

τ²-τ+1/4-5/4=0

τ²-τ+1/4=5/4

(τ-1/2)²=5/4 /√

τ-1/2=±√(5/4)

τ=1/2±√(5/4)

Poznat je izraz:
τn±(1/ τn)~celi broj

Kao što znamo: 
τ 1=0+1* τ
τ2=1+1* τ

Uočimo da su u prvom izrazu koeficijenti 0 i 1 Fibonačijevi brojevi tj. nulti i prvi član Fibinačijevog niza. Slično u drugom izrazu koeficijenti su prva dva člana Fibonačijevog niza. Ako sledimo istu pravilnost, vidimo da je:

τ 3=1+2* τ
τ 4=1+2* τ
τ 5=1+2* τ

Ako bismo ovu pravilnost prikazali opštom formulom, ona bi izgledala ovako:

τ n=Fn-1+Fn* τ
Uzmimo da su a i b dva koeficijenta tj. neka dva uzastopna koeficijenta Fibonačijevog niza.

τ n=a+b* τ

Prvi sledeći bi mogli zapisati kao:

τ n+1=a*τ+b* τ2

Uzmimo u obzir da je τ2=1+1*τ i tako ga zapišimo:

τ n+1=a*τ+b*(τ+1)

τ n+1=a*τ+b*τ+b

τ n+1=τ*(a+b)+b

Pa je u ovom izrazu a+b sledeći član Fibonačijevog niza tj. a+b i b su sledeća dva uzastopna član ovog niza, i time smo dokazali tačnost ove formule.

Fibonačijev niz i τ svuda oko nas

Sa Fibonačijevim brojevima se susrećemo svaki dan, a da to i na opazimo. Fibonačijevi brojevi se pojavljuju na raznim biljkama, od dana klijanja pa sve do cvata. Prilikom rasta mlade biljke, ona se grana i pušta lišće po Fibonačijevim brojevima. Broj latica na cvetu je 3, 5 ili 13, no ima ih i sa više, ali one obično prate tu pravilnost. Malo koja biljka ima 4 ili 6 latica.

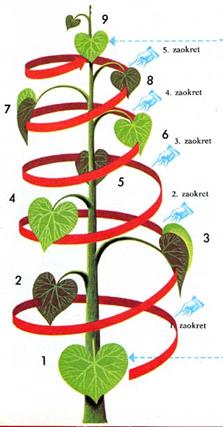
Kada na stabljici biljke rastu novi listovi oni stoje u obliku zavojnice (spirale) oko stabljike. Fibonačijevi brojevi se javljaju kao količnik broja zaokreta spirale i broja međuprostora između listova. Posmatrajmo listove broj 1, 4, 9 koji se nalaze na izabranom pravcu duž stabljike sa listovima:

• Broj međuprostora između listova broj jedan i broj četri je tri. Broj punih zaokreta spirale je dva. Fibonačijev razlomak je 2/3.
• Broj međuprostora između listova broj jedan i broj devet je osam. Broj punih zaokreta spirale je pet. Fibonačijev razlomak je 5/8.
• Broj međuprostora između listova broj četri i broj devet je pet. Broj punih zaokreta spirale od četvrtog do devetog lista je tri. Fibonačijev razlomak je 3/5.

Priroda se brine za pravilan raspored listova na stabljici kako donji listovi ne bi bili zasenjeni donjim i kako bi se svetlo najbolje iskoristilo.
Ovi brojevi se pojavljuju i u semenkama biljaka tj. njihovom rasporedu. Posmatrajmo sledeće slike:

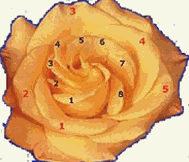
Da mnoge biljke slede spiralni rast matematičke preciznosti, posebno suncokret i kaktusi, odavno je primećeno, ali do sada se nije znalo zašto. Spirale je lako zapaziti. Kaktusova glava je pun ispupčenja a svaka ima čičak. Kod nekih kaktusa se može, polazeći od centra, nacrtati spirala koja povezuje vrh svakog ispupčenja sa sledećim. Tako se mogu dobiti različiti obrasci sa spiralama: sa tri, pet ili osam spirala.

Mehanizam neprekidne podele igra posebnu ulogu u likovnom stvaralaštvu, a ponajviše u oblasti apstraktnih geometrijskih oblika, kombinovanih kroz konstrukciju, funkciju i merilo čoveka u određene prostorne celine.
Leonardo Da Vinci (1451-1519) je pokazao veliki interes za matematiku umetnosti i prirode. On je, kao i Pitagora, uradio kompletnu studiju figure čoveka i pokazao kako su njeni različiti delovi u proporciji zlatnog preseka. Dok u muzici dobro poznavanje nauke o harmoniji prethodi veštini komponovanja, u likovnim umetnostima i arhitekturi, preovlađuje mišljenje da poznavanje proporcija nije neophodno. Na mnogim današnjim svetskim školama za arhitekturu i primenjenu umetnost, problemu proporcija u kompoziciji posvećuje se ozbiljna pažnja.

Literatura:

• Đorđe Petrović, Teoretičari proporcija, Naučna knjiga, Beograd, 1974.
• Frank Land, The Languge of Mathematics, John Murray, London, 1960.
• http://milan.milanovic.org/math/srpski
• http://wikipedia.org

 preuzmi seminarski rad u wordu » » » 

Besplatni Seminarski Radovi