POCETNA STRANA

Leonard Ojler (15. aprila 1707. - 18. septembra 1783.) je Svajcarski matematičar. Ziveo je i radio u Berlinu i Petrogradu. Jedan je od najvećih matematičara u istoriji. Napisao je oko 900 radova. Stvarao je u mnogim oblastima, posebno matematici, fizici i astronomiji.

1 Život u osamnaestom veku

Ojlerova matemati cka karijera po cela je u godini Njutnove smrti. Nije se mogla pronaći povoljnija epoha za genija kao sto je bio Ojler. Analitička geometrija (objavljena 1637. god.) već se upotrebljavala 20 godina, diferencijalni i integralni ra cun oko 50, a Njutnov zakon o svemirskoj gravitaciji, ključ za fizikalnu astronomiju, matematičarima je bio poznat 40 godina. U svakom od ovih podrucja bio je resen veliki broj izolovanih problema, sa nastojanjima za ujedinjenje; ali sistematski napad jos nije organizovan protiv čele matematike, čiste i primenjene, koja je tada postojala. Posebno snazna analitička metoda Dekarta, Njutna i Lajbnica jos nije bila iskorisčena do mogučih graniča, naročito u mehaniči i geometriji.
Pre nego sto predemo na Ojlerov miran, ali interesantan zivot, moramo spomenuti dva dogadaja u njegovo doba koji su utičali na njegovu veliku aktivnost i pomogli mu u odredivanju smera. U osamnaestom veku sveučilista nisu bila glavni ista ziva čki čentri u Evropi. Oni su to mogli postati mnogo ranije nego sto su stvarno postali, a uzrok tome je klasi čna tradičija i ne razumljivo neprijateljstvo prema nauči. Matematika je bila postovana jer se smatrala drevnom znanosču, ali fizika, kao mnogo mlada, bila je sumnjiva. Osim toga, za matematičara se u tada snjem svetu smatralo da mora najveci deo svoga vremena utrositi na učenje daka; njegovo istrazivanje, ako se uopste time bavio, smatralo se nekorisnim luksuzom.
Vodstvo su preuzele razne kraljevske akademije potpomognute plemenitim vladarima. Matematika duguje veliku zahvalnost Fridrihu Velikom i Katarini Velikoj za njihovu veliku liberalnost. Zahvaljujuci njima osamnaesti vek bio jedan od najaktivnijih perioda u istoriji nauke. U slu čaju Ojlera, Berlin i Petrograd dali su snagu matemati čkom stvarala stvu. Oba ova stvarala čka sredi sta zahvaljuju svoju inspiračiju neumornoj Lajbnicovoj ambiciji. Akademije za koje je Lajbnic izradio planove pruzile su Ojleru mogučnost da postane najplodniji matematičar svih vremena.
Berlinska akademija polako je umirala kroz 40 godina bez pametnih ljudi, kada joj je Ojler na inicijativu Fridriha Velikog ponovo udahnuo zivot; a Pet-rogradska akademija, koja zbog smrti Petra Velikog nije bila organizovana u skladu sa Lajbnicovim programom, bila je solidno organizovana od njegovog naslednika.
Te akademije nisu bile sli čne nekim dana snijm kojima je glavna funkčija da nagraduju svoje članove za dobro izvrsen posao; one su bile istrazivačke or-ganizacije koje su placale svoje istaknute članove da vrse naučna istraz ivanja. Osim toga plate i benefičije bile su dovoljne da su čovek i njegova porodica mogli pristojno da zive. U jednom je periodu u Ojlerovoj kuči zivelo čak osamnaest osoba; ipak je on zaradivao toliko da je sve mogao pristojno da izdr zava. I kona čno, privla čnost zivota akademika u osamnaestom veku bila je i u tome sto su njegova deča, ako su uop ste ne sto vredela, imala dobru odsko čnu dasku u svet. To nas dovodi do drugog vaznog uticaja na Ojlerovu opsirnu matematičku proizvodnju. Vladari koji su platili račun prirodno su zeleli da dobiju ne sto kao dodatak apstraktnoj kulturi za svoj novac. Ali mora se naglasiti da vladari kada su jedanput dobili zadovoljavajuci prihod za svoje ulaganje nisu insistirali da njihovi slu zbeniči utro se ostatak svoga vremena na "proizvodnom"radu; Ojler i Lagranz i drugi akademici bili su slobodni da rade ono sto zele. Nije bio vidljiv ni bilo kakav jači pritisak da bi se iznudili neki hitni praktični rezultati koje bi drzava mogla upotrebiti. Za razliku od mnogih istazivačkih instituta danas, vladari osamnaestog veka sugerisali su sasvim malo i pustili nauku da sledi svoj put.

2 Životni put Leonarda Ojlera

2.1 Prvi koraci i usmerenje

Leonard Ojler, sin Paula Ojlera i njegove zene Margarite Bruker, verovatno je največi naučnik koga je Svajčarska dala. Rodio se u Baselu 15. aprila 1707. godine, ali je več iduče godine presao s roditeljima u obliznje selo Riečhen, gde mu je otač postao kalvinistički pastor. Paul Ojler je i sam bio odličan matematičar i u čenik Jakoba Bernulija. Otac je imao nameru da Leonard podje njegovim stopama i da ga nasledi u seoskoj črkvi, ali je, na srecu pogres io i dečaka učio matematku.
Ojler je od najranijeg detinjstva znao sta zeli. Uprkos tome, on je poslu sno po stovao volju oča i upisao se na Sveu čili ste u Bazelu, da studira teologiju. U matematici je dovoljno napredovao da bi privukao paznju Johana Bernulija, koji je nesebično davao mladicu privatne časove jednom nedeljno. Ojler bi ostatak nedelje potrosio spremajuci se za iduci čas tako da bi sledeceg puta mogao postaviti sto vise pitanja svom učitelju. Danijel i Nikolaus (Johanovi sinovi) brzo su primetili njegovu inteligenciju i sposobnost i postali su njegovi najbolji prijatelji.

Leonard je mogao uzivati sve dok nije dobio diplomu zrelosti 1724. godine, u sedamnaestoj godini, kada je njegov otac insistirao da napusti matematiku i potpuno se posveti teologiji. Ali je otac popustio kada su mu Bernulijevi rekli da je njegov sin predodredjen da bude veliki matematicar. I premda se proročanstvo potpuno ispunilo, takvo vaspitanje je na Ojlera imalo utičaja do kraja zivota. Sto je bio stariji, sve se vi se secao poziva svog oca.
Prvi samostalan rad Ojler je uradio kada je imao devetnaest godina. Nije dobio nagradu ali je dobio posebno priznanje za resenje jarbola na brodovima. Kasnije je nadoknadio taj gubitak, jer je dvanaest puta osvojio nagradu.
Svestan da je rodjeni matematičar , Ojler se borio za mesto profesora u Bazelu. Kada nije bio izabran, nastavio je sa studiranjem hrabren nadom da ce se pridruziti Danijelu i Nikolausu Bernuliju u Petrogradu. Oni su se ljubazno ponudili da ce Ojleru naci mesto u Akademiji.
U tom periodu činilo se da je Ojler bio za čudo indiferentan sta ce raditi, samo da bude nesto naučno. Kada su Bernulijevi pisali o perspektivnom otvaranju medicinske sekcije na Petrogradskoj akademiji, Ojler se u Bazelu upisao na filozofiju i slusao je predavanje iz medicine. Ali čak i na tom polju on nije mogao biti po strani od matematike jer je fiziologija uha zahtevala matematička ispitivanja zvuka.

2.2 Zivot u Rusiji

Ojler je dobio sluzbeni poziv u Petrograd 1727. godine da bude saradnik i medicinskoj sekciji Akademije. Ojlerovo veselje je ubrzo prestalo. Onoga dana kada je stupio na tlo Rusije, umrla je liberalna Katarina I.
Katarina je bila ljubavnica Petra Velikoga pre nego sto je postala njegova zena i čini se da je bila u mnogim pogledima pametna zena; ona je za dve godine svoga vladanja ostvarila Petrovu zelju o osnivanju Akademije. Nakon smrti Katarine I vlast je pre sla u ruke neobično okrutne struje koja je vladala u ime maloletnog čara (koji je, mozda na srecu, umro ranije nego sto je počeo vladati). Novi vladari gledali su na Akademiju kao na suvisni luksuz i u toku nekoliko meseci uspeli su da je zabrane. Takvo je stanje bilo kada je Ojler do sao u Petrograd. U toj zbrci nije nista rečeno o stanju medicinskog mesta na koje je pozvan i on se ubacio u matematičku sekciju jer su se posle nekog vremena stvari sredile.
U toku sest godina on je neumorno radio, ne samo zbog toga sto je bio sav u matematici vec delimično i zbog toga sto se nije usudio voditi normalni drustveni zivot jer su spijuni bili na sve strane.

Godine 1733. Danijel Bernulije se vratio u Svajcarsku i Ojler je u dvadeset i sestoj godini zauzeo vodeči polozaj matematičara na Akademiji. Osecajuci da ce ostati u Petrogradu ceo svoj zivot, Ojler je odlučio da se ozeni. Odabranica je bila Katarina, kcerka slikara Gsella, kojeg je Petar Veliki poveo sa sobom u Rusiju. Političke prilike postale su jos gore i Ojler je očajno, vise nego ikada, zeleo da pobegne. Ali brzim dolaskom dece jednog za drugim eu-ler je bio sve vi se vezan i izlaz je na sao u neprekidnom radu. Stalna opeznost silila ga je na neprekidni rad.
Ojler je bio jedan od nekoliko velikih matematičara koji je mogao raditi svuda i pod svakakvim uslovima. Veoma je voleo decu (imao ih je trinaestoro, ali je petoro umrlo u ranom detinjstvu) i često je pisao svoje bele ske s detetom na krilu dok su se starija deca igrala oko njega. Lakoca kojom je on pisao najte ze matematičke probleme neverovatna je. Jos se spominju mnoge legende o njegovom stalnom izmisljanju ideja. Bez sumnje, neke su preterane, ali se tvrdi da je Ojler mogao napisati matematički problem u pola sata ili izmedju dva obroka.
Kada je umro car (dečak), Ana Ivanovna, Petrova necaka postala je 1730. godine carica, i sto se tiče Akademije, stvari su se znatno pobolj sale. Ali pod posrednom vladavinom Aninog ljubavnika Ernesta Johna de Birona Rusija je trpela najkrvaviju vladavinu u svojoj istoriji. Ojler se smirio i povučeno radio nekih deset godina.

3 Ojlerov doprinos u matematici

Ojler je do sao do zapazenih rezultata u svim oblastima matematike koje su u to vreme postojale. Svoja otkrica objavljivao je ne samo u člancima razli čitog obima več i u mnogim obimnim priručnicima, gde je sreden i kodifikovan materijal do kojeg su dosle ranije generačije. U nekim oblastima Ojlerovo izlaganje moze se smatrati skoro potpuno zavrsenim. Primer je na sa sadasnja trigonometrija sa svojom koncepčijom trigonometrijskih veli čina kao koli čničima i sa svojom simbolikom, koja potiče iz Eulerovog dela Uvod u analizu beskonacnih velicina, 1748.god. Ogromni autoritet njegovih priručnika u činio je da se u algebri i analizi učvrste njegove oznake.

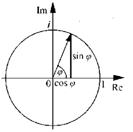U dva toma Uvoda obuhvaceno je veoma mnogo različitih pitanja. Tu se nalazi Ojlerovo izlaganje beskonačnih redova, medu kojima redovi za ex, sinx i cosx i relačija etx = cosx + isinx poznata kao Ojlerova formula.

Ako se x zameni sa n dobija se Ojlerov identitet el7T + 1 = 0 koji je zna čajan po tome sto daje vezu izmedu 5 izuzetno vaznih matemati č kih konstanti e, i, n, 1
i 0.
Ispitivanje krivih i povrsi pomoču njihovih jednačina izvodi se tako slo­bodno da mo zemo Uvod smatrati prvim ud zbenikom analiti čke geometrije. Ovde nalazimo i algebarsku teoriju eliminačije. Razlaganje bro jeva na sabirke je deo Uvoda koji posebno zadivljuje.

3.2 Ojlerovi integrali

Drugi veliki i sadrzajno bogat Ojlerov priručnik je Diferencijalni račun, 1755. Posle ovog priru čnika pojavila su se tri toma Integralnog računa, 1768­1744. Tu nalazimo ne samo na s elementarni diferencijalni i integralni račun vec i teoriju diferenčijalnih jednačina, Tejlorovu teoremu sa mnogim primenama, Ojlerovu teoremu za sumiranje i Ojlerove integrale r i B :

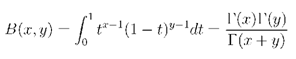
r(z) = tz-1e-tdt Jo
Potpuni uvod u algebru (1770. god.) napisan je na nemačkom jeziku i Ojler ga je diktirao slugi jer je tada bio slep. Izlaganje je u toj knjizi dovedeno do teorije jednač ina trečeg i četvrtog stepena.

Ojlerovo delo Metode za nalaženje krivih linija koje poseduju osobine minimuma ili maksimuma pojavilo se 1774. godine.

3.3 Ojlerova teorema za pravilne poliedre

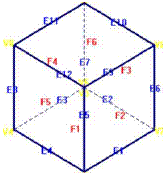
Medu poznatijim radovima je i teorema koju je on otkrio, a u kojoj je uspostavljena relačija izmedju broja temena V, strana F i iviča E zatvorenog poliedra :

V+F-E=2

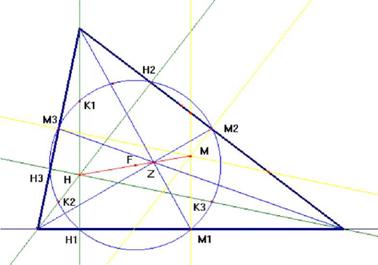
3.4 Ojlerova prava

U bilo kom trouglu vazi da su ortocentar H, srediste opisanog kruga M i teziste Z koninearne tacke i vazi HZ = 2ZM.

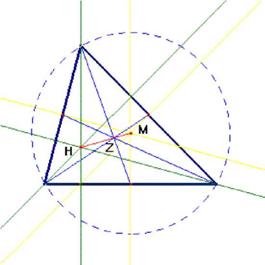
3.5 Devet tačaka Ojlerovog kruga

Sredista stranica, podnožja visina i sredista duzi odredenih temenima i ortocenrom bilo kog trougla pripadaju jednom krugu.

3.6 Ojlerova konstanta

Ojlerova konstanta

U njegovom radu sa beskonačnim redovima proučavao je konstantu

koja nosi njegovo ime i pokazao kako se koristi za procenu sume beskonačnog reda

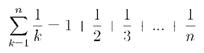
buduči da je

3.7 Poznate Ojlerove oznake

1736. godine Ojler je uveo simbol e za transcendentni broj koji se definise kao granična vrednost

1748. godine uveo je oznaku

i = v—1

3.8 Problem Keningsberskih mostova

Nekoliko Ojlerovih članaka posvećeno je zanimljivoj matematici. Jedan od njih je Problem Keningsberskih mostova.
Kroz centar nekadasnjeg pruskog grada Keningsberga, danas Kalinjingrada, protiče reka Pregel.

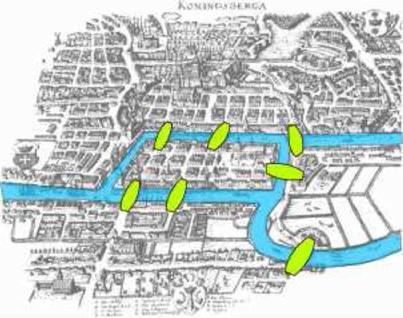
Na reči su dva ostrva povezana medjusobno i sa obalama reke sa sedam mostova. Priča se da su stanovnici Keningsberga zabavljali pokusavajuci da obidju svih sedam mostova, a da pri tome preko svakog predu tačno jedanput. Medutim uprkos svim nastojanjima nikome to nije poslo za rukom.Isto tako niko nije bio u stanju ni da dokaze da je tako ne sto neizvodljivo. Prvi koji je u tome uspeo bio je Ojler. Ojlerov dokaz ne postojanja odgovarajuce setnje Keningber skim mostovima smatra se prvim rezultatom, a samim tim i početkom teorije grafova. U Eulerovu čast čitava jedna klasa grafova dobila je ime Ojlerovi grafovi.

4 Jos neka Ojlerova dela

Naro čitu paznju Ojler je poklanjao astronomiji, ta čnije teoriji kretanja Meseca. Napisao je Teoriju kretanja planeta i kometa, 1774. god. koja se svrstava u oblast nebeske mehanike. S tim njegovim radom su u vezi njegova ispitivanja o privla čenju elipsoida (1738. god.).

Ojlerovo delo Metode za nalaženje krivih linija koje poseduju osobine maksimuma ili minimuma pojavilo se 1774. godine.

Ako njegovi napori da dokaze postojanje korena algebarske jednačine nisu doveli do neoborivog dokaza, oni otvaraju put njegovim nastavlja čima, posebno Lagranžu, inače njegovom učeniku po mnogim pitanjima. Iako su razmenili bogatu prepisku, Ojler i Lagranz se, međutim, nikad nisu sreli. Radovi iz vise aritmetike Lagranza i Ojlera usko su povezani, i uopste, Ojler je otvarao put a Lagranz je pojednostavljivao ili uopstavao.
Godine 1909. Svajcarsko drustvo za prirodne nauke počelo je sa sakupljanjem i objavljivanjem Ojlerovih razbacanih memoara uz finansijsku pomoc mnogih ličnosti i matematičkih drustava sirom sveta s pravom tvrdeći da Ojler pripada čitavom civilizovanom svetu, a ne samo Švajcarskoj.

Literatura