Генијални математичар,физичар и астроном Исак Њутн родио се на Божић 1642. године у месту Вулсторп у Енглеској. Рођен је исте године када је умро Галилеј.
Пореклом је из сиромашне, независне сељачке породице. Један је од највећих умова свих времена, био је професор Универзитета у Кембриџу, управитељ ковнице новца и члан Парламента. Бесмртан је по томе што је:
-написао Општу аритметику у којој стоји и : “Да би се решио неки проблем, треба га само превести са обичног језика на језик алгебре.”
-открио закон гравитације(Њутнов закон гравитације);
-извео Кеплерове законе;
-пронашао и објаснио три основна закона кретања класичне механике(Њутнова механика);
-дао основе инфинитезималног рачуна-независно од Лајбница;
-објаснио многе светлосне појаве и открио њихове законе;
-објаснио спектар боја сунчеве светлости итд.

Њутнов утицај на његове савременике је тешко оценити, јер се он стално колебао да ли да објављује своја открића. Први је испитао закон свемирске гравитације 1665-1666., али га је објавио тек 1686. године, када су штампани његови Принципи, где је овоме посвећен већи део. Његова Општа аритметика (Arithmetica universalis), која је штампана 1707. године, састављена је од предавања из алгебре, у периоду између 1673. и 1683. године. Његов рад о редовима из 1669. године, сдржан је у писму Олденбургу из 1676. године, а штампан је тек 1711. године. Њутнов рад о квадратури кривих из 1671. године штампан је тек 1704. године и тада се у јавности први пут појавила његова теорија флуксија. Метода флуксија појавила се у јавности тек после његове смрти 1736. године.
Преминуо је 1727.године у Лондону.

Рани дани Исака Њутна

Родио се пре времена. При рођењу је био слаб и мали да су многи сумњали да ће преживети. Пошто је Њутнов отац умро пре него што се он родио, његова мајка се поново удаје и оставља га као трогодишњака код баке.
Пошто као дете није био снажан, избегавао је грубе игре својих вршњака и пронашао је своју властиту разоноду где се први пут показује његов геније.
Ненадмашна генијалност коју је Њутн показао као проналазач у мистеријама светла, огледа се у оштроумности његових дечачких забава. Фењери, којима је плашио сељаке по ноћи, одлично израђена механичка лутка која се креће,коју је он сам направио,млин са прождрљивим мишем(донео му највећу зараду) који је истовремено био и млин и погонска снага и пшеницу млео у брашно, цртежи, сунчани сат и дрвени сат који са сам навијао само су неке од ствари којима се Исак као дечак занимао. Као додатак свим доказима талента, Њутн је све тајне и необичне примедбе бележио у нотес.
Његов ујак,свештеник Вилијам, први је уочио да Њутн није обичан дечак. Успео је да наговори Њу тнову мајку да га пошаље у Кембриџ уместо да га држи код куће, како је планирала, да би јој помогао у управљању фарме, након њеног повратка после смрти њеног другог мужа. Тада је Њутну било петнаест година. Још када је био у грантхамској школи и касније када се спремао за Кембриџ становао је са Кларком,сеоским апотекаром. У поткровљу апотеке је нашао хрпу старих књига које је он гутао. За Кембриџ одлази 1661. године са деветнаест година.

Дани у Кембриџу

Учио је у Кембриџу код Исака Бароа, теолога и математичара, за кога се тврди,иако је био изванредан и оригиналан математичар, да је имао несрећу да буде јутарња звезда која је наместила њутново сунце. Баров је признао да је дошао већи од њега и 1669. године је поднео оставку на место професора математике и предао своју професорску катедру свом ученику(то је веома значајна појава у академском животу). Тако је јавно признао Њутнову предност.
Њутн је остао у Кембриџу до 1696. године када је постао инспектор, а касније и руковдилац ковнице новца.
Прве две године студија утрошио је на савлађивање основа математике. Из његовог студентског живота позната нам је чињеница да је три године постављао темеље читавог свог каснијег рада у науци и математици и да се због напорног рада разболео.

На раменима генија

Њутну се преписује изрека:”Ако сам видео мало даље од других, то је због тога што сам стајао на раменима оријаша.” Међу највећим су били Декарт, Кеплер и Галилеј. Од Декарта је наследио аналитичку геометрију, коју је на почетку сматрао тешком, од Кеплера три основна закона о кретању планета, од Галилеја је узео прва два, од три закона кретања, који су постали основа његове властите динамике.
Његов изузетан ауторитет створили су, углавном, његови Математичкипринципиприроднефилозофије(Philosophiae naturalis principia mathematica,1687). То је обимна књига која садржи аксиоматску изградњу механике и закон гравитације, тј. закон који управља падањем јабуке на земљуи кретањем Месеца око Земље.
Њутн је строго математички извео Кеплерове законе кретања планета који су емпиријски били установљени полазећи од закона гравитације о привлачењу које је обрнуто пропорционално квадрату растојања.
Њутнов закон опште гравитације гласи:
Између свака два тела(две тачкасте масе)делује привлачна,гравитациона сила, која је сразмерна производу њихових маса, а обрнуто сразмерна квадрату њиховог међусобног растојања.
Гравитациона сила делује дуж праве која пролази кроз центре два тела.

$F=\gamma\frac{m_{1}\cdot m_{2}}{r^{2}}$

где:
F је интезитет гравитационе силе између два тела
γ је гравитациона константа, чест и симбол g
т1,т2 су масе првог и другог тела
r је међусобно растојање два тела(у идеалном растојање измађу центара две масивне сфере) .
У Међународном систему јединица(SI јединице), F се мери у њутнима(N), т1`,т2 у килограмима(kg), r у метрима(т), а вредност константе γ је приближно једнака 6.67*10-11Nт2kg-2(њутн пута метар квадратни по килограму квадратном).
Њутн је са становишта динамике дао објашњење плиме и многих појава које настају при кретању небеских тела. Решио је проблем два тела за сферу и поставио је темеље у теорији потенцијала. Његово аксиоматско разматрање изискивало је апсолутност простора и апсолутност времена. Он је владао анализом,па је било тешко сагледати геометријску форму његових доказа. Анализу је називао теорија флуксија.

Њутнова јабука

Постоји популарна прича о томе како је једна јабука која је пала са дрвета инспирисала Њутна да формулише његову теорију гравитације. Илустратори и цртачи карикатура иду још и даље, сугерушући да је јабука у ствари пала Њутну право на главу и да је тај ударац на неки начин учинио га свесним гравитационе силе. Џон Кондуит, Њутнов помоћник, у време док је он био управник Краљевске ковнице новца, и муж Њутнове нећаке, пишући о Њутновом животу описао је овај догађај на следећи начин:
Године 1666. он је опет напустио Кембриџ и одмарао се код своје мајке у Линколнширу. Док се замишљено шетао по башти, пала му је на памет мисао да сила гравитације (која преноси јабуку са дрвета на земљу) није ограничена на неку одређену удаљеност од Земље, него да та сила допире много даље него што ми обично мислимо. Зашто не толико далеко као што је Месец удаљен и, ако је то тако, она мора утицати на његово кретање, рецимо задржавати Месец на његовој орбити, после чега се бацио на прорачунавање ефеката ове његове претпоставке.
Питање није било да ли гравитација постоји, него да ли њено деловање допире тако далеко од Земље да би могла да буде такође и сила која задржава Месец на његовој орбити. Њутн је показао да, ако сила гравитације опада (обрнуто је сразмерна) са квадратом растојања, на основу тога може се израчунати период Месечеве орбите, и то у веома доброј сагласности са измереним подацима. Он је даље претпоставио да је иста сила одговорна и за кретања планета по њиховим орбитама, као и друга орбитална кретања и, у складу с тиме, назвао је ову силу “универзална гравитација”.
Њутнов савременик, писац Вилијам Стакли забележио је у својим „Сећањима из живота Сер Исака Њутна“ разговор са Њутном у Кенсингтону, у којем се Њутн подсећа како је: „Недавно је представа о гравитацији дошла у његове мисли. Било је то приликом пада једне јабуке са дрвета“, рекао је Њутн у једном замишљеном расположењу. „Зашто је то тако да јабука увек пада вертикално са дрвета на Земљу?“, питао је Њутн сам себе. „Зашто се не креће на страну или навише, него увек пада преме центру Земље?“.
На сличан начин и Волтер пише у свом „Есеју о Епској поезији“ (1727), „Сер Исак Њутн ходајући по својој башти, помислио је по први пут на свој систем гравитације, гледајући једну јабуку како пада са дрвета“.
Ова објашњења представљају вероватно преувеличавања Њутнове сопствене приче о томе како је седео поред прозора своје куће у Вулстроп Манору и гледао јабуку како пада са дрвета.
За многа стабла тврди се да су дрво јабуке коју је Њутн описао. У Краљевској школи у Грантаму тврде да је школа неку годину касније добавила себи стабло, тако што га је ишчупала са кореном и пребацила у управникову башту. Особље „Националног труста за надзор над местима од историјске важности и природних лепота“, у чијем је власништву данас Њутнова кућа Вулстроп Манор, оспоравају ово и тврде да је дрво које се налази у њиховој башти оно које је Њутн описао. Потомак оригиналног дрвета јабуке може се видети како расте испред главне капије Тринити Колеџа, у Кембриџу, нешто ниже од собе у којој је Њутн становао када је ту студирао.

Њутнови закони

Њутонови закони су скуп од три основна закона класичне физике. Они описују везу између кретања тела и сила које делују на тело и први их је представио Исак Њутн. Објављени су у књизи Philosophiae Naturalis Principia matematica. Ови закони чине темеље класичне механике. Њутн их је користио да опише примећене резултате опита у вези кретања тела.

Први закон: Закон инерције

На латинском, у оригиналу, Њутн га је записао:
Lex I:
Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quatenus a viribus impressis cogitur statum illum mutare.

Тело остаје у стању мировања или се креће константном брзином ако на њега не делује ниједна сила, односно је резултантна сума свих сила на тело таква да се силе потиру.
$\sum_{i=1}^ n \overrightarrow{F_i} = \overrightarrow{0}$

Овај закон описује принцип инерције и може се исказати у другачије-Тело на које не делују силе има тежњу да настави кретање истим смером и брзином.

Други закон: Закон силе

Овај закон је Њутн написао на латинском овако:
Lex II:
Mutationem motus proportionalem esse vi motrici impressae, et fieri secundum lineam rectam qua vis illa imprimitur.

Величина силе на неко тело управо је сразмерна убрзању и маси тог тела. Смер силе има исти смер као и убрзање.

$\overrightarrow{F}= m \cdot \overrightarrow{a}$
F је сила, m маса, a убрзање.
Овај закон описује чињеницу да је промена кретања, убрзање, неког тела могућа једино дејством силе и повезује силу која делује на тело са масом тела и убрзањем којем је тело изложено.

Трећи закон: Закон акције и реакције

Текст закона записан на латинском је:
Lex III:
Actioni contrariam semper et æqualem esse reactionem: sive corporum duorum actiones in se mutuo semper esse æquales et in partes contrarias dirigi.

За сваку акцију на неко тело постоји и реакција. Исте је величине али супротног смера.

$\overrightarrow{F_1} = -\overrightarrow{F_2}$

Ови закони су важећи само у класичној механици, где је брзина много мања од брзине светлости а маса тела пуно већа него величина атомских делова (електрон, протон, неутрон). У случају изузетно великих брзина, упоредивих са брзином светлости, или изузетно малих маса, упоредивих са масом атома, појављују се други ефекти који се прецизно описују законима квантне механике. Из закона квантне механике се добијају Њутнови закони тако што се апроксимира да су брзине бесконачно мале спрам брзине светлости.

Бесмртан у двадесетчетвртој или пре

Када се налазио у свом родном месту, у селу где је побегао од куге која је харала по Кембриџу, 1665-1666. открио је своју општу методу. Из тог времена потичу његове основне идеје о свемирској гравитацији, као и о сложености састава светлости. Све је постигао пре него што је напунио двадесет и пет година.
Рукопис из 1665. показује да је Њутн, када је имао двдеасет и три године, довољно развио принципе диференцијалног рачуна, да је могао пронаћи тангенту и накривљеност у свакој тачки непрекидне криве. Назвао је своју методу “флукс” . Томе је претходило његово откриће биниомне теореме, главне степенице према потпуно развијеном диференцијалном рачуну. Биномна Теорема генерализује једноставне резултате као (а+b)2=a2+2ab+b2 , (a+b)3=a3+3a2b+3ab2+b3 , итд. што добијамо директним рачуном; наиме

n n(n-1) n(n-1)(n-2)
(а+b)n=an+ — an-1b+ ——— an-2b2+ ————— an-3b3 + ...
1 1 x 2 1 x 2 x 3
Ако је п један од позитивних целих бројева ред се завршава после тачно п+1 разломака. То се лако може доказати математичким закључивањем.
Њутново откриће флуксије у уској је вези са његовим проучавањем бесконачних редова по Валисовој Аритметици . Том приликом Њутн је уопштио биномну теорему и за случајеве када су изложиоци разломци и негативни бројеви,па је тако открио и биномни ред. То му је олакшало проширење његове теорије флуксија на “све” функције, било да су трансцедентне или алгебарске. “Флуксије” су означаване са · , која је стављана изнад слова, и биле су коначне величине, брзине, а слова без тачке означавала су “флуенте”.

Математичка истраживања

Њутн и Лајбниц су открили инфинитезимални рачун независно један од другог, користећи сваки своју сопствену, јединствену, нотацију (као што су већина матеметичара то и чинили у то време). Мада је Њутн разрадио свој метод годинама пре Лајбница, он није објавио о томе скоро ништа све до 1693., и потпуни увид у свој инфинитезимални рачун пружио је тек 1704. . У међувремену, Лајбниц почиње да објављује потпуни опис свог метода 1684. Поврх тога, Лајбницова нотација и “инфинитезимални метод” постају опште прихваћени на континенту, а после 1820. и у Британској империји. Њутн је тврдио да је он био нерад да објави његов инфинитезимални рачун бојећи се да би због тога могао бити исмеван. Почев од 1699. , други чланови краљевског друштва оптужују Лајбница за плагијат, а овај спор избија пуном снагом у 1711. . Тако започиње горка Њутнова расправа са Лајбницом око приоритета открића инфинитезималног рачуна, која ће их пратити скоро целог живота, све до смрти Лајбница. Ова расправа створиће поделу између математичара Британије и континенталне Европе, која је можда за читав век успорила напредак математике у Британији.
Њутну је одато признање за откриће генерализоване биномске теореме, важеће за било који експонент. Он је открио Њутнове идентитете, Њутнов метод, дао значајан допринос теорији коначних разлика, и био први који је користио разломачке индексе и употребио координатну геометрију да дође до решења Диофантинових једначина.
Њутн је писао о конусним пресецима и о кривим линијама у равни трећег реда. У Пребројавању линија трећег реда (Enumeratio linearum terti ordinius, 1704.) начинио је класификацију равних кривих трећег степена, а садржала је 72 облика. Тада је пошао од своје теореме која казује да се свака кубна крива може добити из “дивергентне параболе” y2=ax3 + bx2 + cx + d при централном пројектовању једне равни на другу. То је био први значајнији нови резултат до којег се дошло применом алгебре на геометрију, јер су сви ранији радови били обичн преводи Аполонија на језик алгебре. Њутну приоада и метода за добијање приближних вредности решења нумеричких једначина. Он је то објаснио на примеру x3-2x-5=0 где је као решење дате једначине добио x=2,09455147.
Извршио је апроксимацију парцијалних сума хармонијских низова помоћу логаритама (претходник Ојлерове сумирајуће формуле) и био први који је користио са сигурношћу математичке редове и обрнуте математичке редове. Он је такође открио и нову формулу за број пи (π).
У време када је био професор математике на Лукасовој катедри, сваки предавач на Кембриџу или Оксфорду требало је да буде рукоположени англикански свештеник. Међутим, термин Лукасовски професор подразумевао је и додатак “не бити активан у цркви” (што се подразумевало да би се добило више времена за науку). То је био Њутнов аргумент, да би га због тога требало изузети од рукоположења, и Чарлс II, чије је одобрење за ово било потребно, прихватио је овај његов аргумент. Тако је избегнут конфликт између Њутнових религијских погледа и англиканске ортодоксије.

Диференцијални рачун

Општу методу диференцијације и интеграљења засновану на потпуном схватању инверзности ова два процеса, могли су пронаћи тек они људи који су овладали како геометријским методама Грка и Кавањерија, исто тако и алгебарским методама Декарта и Валиса. Ти људи су се могли појавити тек после 1600. и они су се појавили у личностима Њутна и Лајбница. Доста је написано о приоритету тога открића. Установљено је да су Њутн и Лајбниц до својих метода дошли независно један од другог.
Њутн је први открио анализу (1665-1666.), а Лајбниц(1673-1676.), али је Лајбниц први штампао своје радове(штампао их у времену од 1684-1686.), а Њутнови радови су објављени тек после његове смрти, између 1704. и 1736. године.
Диференцијални рачун и диференцирање проучавају промене реалних функција при променама независне варијабле, тј. независне променљиве. Полази се од проблема налажења тангенте на криву, који је први објавио Исак Бароу (Lectiones geometricae, 1670). Исак Њутн је открио метод (1665-1666.) и сугерисао Исаку Бароу да методу укључи у уџбеник. У својој првобитној теорији, Њутн је посматрао функцију као променљиву, флуентну количину, и разлику, или износ промене, назвао флукс. Дефинисао је нагиб криве у тачки као прираштај тангенте на ту криву у малој околини дате тачке. Данас веома познату биномну теорему Њутн је применио да нађе гранични случај, што значи да је диференцијални рачун Њутну био потребан за бесконачне низове. Употребио је ознаке икс, односно ипсилон са тачком изнад ( $\dot{x}, \dot{y}$ ) за флукс, и исто са две тачке изнад ( $\ddot{x},\ddot{y}$ ) за флукс флукса. Тако, ако је x = f(t), где је t време потребно телу да би се прешло пут х, тада је флукс икса тренутна брзина, а флукс флукса је тренутно убрзање. Навешћемо пример како је Њутн објашњавао своју методу (из Метода флуксија, 1736.). Промехљиве су флуенте и означавају се са v, x, y и z, а ”брзине којиима се свака флуента увећава услед изазваног кренања(које могу назвати флуксијама или једноставно брзинама или хитринама)ја ћу представљати тим истим словима и тачкама изнад.“ . Бесконачно мале величине Њутн је називао “моментима флуксије” и означавао их је са vo, vx, vy и vz са тачкама изнад, где oозначава “бесконачно малу количину”.
Лајбниц је такође открио исту методу 1676. године, објавио је 1684. Њутн је није објавио све до 1687. (у Philosophiae Naturalis Principia Mathematica). Зато се развила горка расправа око приоритета открића. Заправо, данас је познато, обојица су дошли до истог открића независно један од другог. Савремена нотација дугује Лајбицу dy/dx и издужено S (од „сума”)за интеграл.

Интегрални рачун

Интегрални рачун и интеграција користе се за израчунавање површина, запремина тела, дужина криве, тежишта, момента инерције. Вуче корене још од Еудокса Книдског, грчког астронома и математичара, и његове методе „исцрпљивања“ из периода око 360. п.н.е. Архимед је у свом делу „Метода“ развио начин налажења површина ограничених кривама, разматрајући их подељене многобројним паралелним линијама и проширио идеју на налажење запремина неких тела. Због тога га неки називају оцем интегралног рачуна.
Почетком 17. века, поново се појавио интерес за мерење запремина интегралном методом. Кеплер је користио процедуре налажења запремина тела узимајући их као композицију бесконачног скупа инфинитезимално (бесконачно) малих елемената (Stereometrija doliorum, 1615.). Ове идеје је поопштио Каваљери у свом делу Geometria indivisibilibus continuorum nova (1635), у којем је употребио идеју да се површина састоји из недељивих линија, а запремина од недељивих површина. То је данас познати Каваљеров принцип, а такође то је био и концепт Архимедове Методе. Џон Валис у свом делу Бесконачна аритметика (Arithmetica ifinitorum, 1655) је аритметизовао Кавалијерове идеје. У том раздобљу су инфинитезималне методе интензивно кориштене за тражење дужина кривих и површина.
Негде у данашње време, интеграција се почела тумачити једноставно као операција инверзна диференцирању. Коши је 1820-их диференцијални и интегрални рачун поставио на сигурније основе заснивајући их на лимесу. Диференцирање је дефинисао као граничну вредност количника, а интегрирање као граничну вредност збира. Дефиницију интеграла помоћу граничне вредности уопштио је Риман .
У двадесетом веку, схватање интеграла је проширено. У почетку, интегрирање се односило на елементарну идеју мерења (мерење дужина, површина, запремина) са непрекидним функцијама. Са појавом теорије скупова, функције су се почеле третирати као пресликавање, не обавезно непрекидно, и појавило се општије и апстрактније схватање мере.
Теорије математичке анализе се обично проучавају у контексту реалних бројева, комплексних бројева, и реалних и комплексних функција. Међутим, оне се могу дефинисати и проучаватии у било ком другом простору математичких објеката, који има дефинисану близину (тополошки простор) или специфичније раздаљину (метрички простор).
Са две основне основне идеје, dx/dyи ∫ f(x)dxод интегралног рачуна можемо описати основну теорему интегралног рачуна.
Замислимо непрекидну, несаломљиву криву чија је једначина y=f(x) у координатном систему.

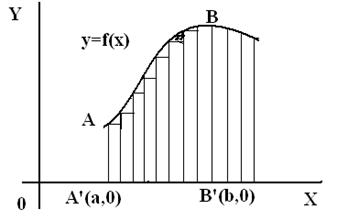
Треба пронаћи површину између криве, осе x и двеју дужи АА’, BB’ повучених на осу х из тачака А и B на кривој. Удаљености ОА’, ОB’ односе се на a, b тј. координате тачака А и B су, редом, (а,0) и (b,0). Радимо како је учинио и Архимед, делимо одређену површину на правоугаонике , не гледајући на троугаоне остатке, сабирајући површине свих правоугаоника и на крају израчунавајући граничну вредност овог збира, као и број правоугаоника који се бесконачно повећава. Поставља се питање:”Како можемо да израчунамо граничну вредност?” .
Прво, пронађимо ∫f(x)dx. Нека је резултат F(x). Када заменимо а и b добијамо F(а) и F(b). Заменимо прво другим и добијамо F(b)-F(a). То је тражена површина. Утврдили смо да је тражена површина, која је гранични број врсте описане у вези с Архимедом, дата у F(b)-F(a). Симбол ∫ је старински s, прво слово од речи Suma.
Када спојимо све, добијамо:
b
∫ f(x)dx=F(b)-F(a)
a

где је а доња гранична вредност, b горња гранична вредност.
Данас је нама ова формула позната као Њутн-Лајбницова формула. Већ смо нагласили да су до ње дошли независно један од другог.

Интерполациони Њутнов полином са подељеним разликама

Задати функцију y=f(x) значи свакој допустивој вредности аргумента х придружити одговарајућу вредност у. Често је одређивање вредности у у вези са многим потешкоћама, па је могуће добити само невелику таблицу вредности функције. Зато је погодно, некада и неопходно, заменити функцију f(x) приближном формулом, тј. функцијом g(x) која је блиска у неком смислу функцији f(x)и пишемо f(x)≈g(x). Блискост функција се постиже одговарајућим избором слободних параметара (c0,…,cn) функције g(x).
При линеарној апроксимацији функција g(x) тражи се у облику генерисаног полинома,
g(x)=c0φ0(x)+…+cnφn(x),

где су φ0(х),...,φп(х) линеарно независне функције које чине основни систем функција.
Када се параметри апроксимације c0,…,cn одређују тако да су вредности функција f(x) и g(x) једнаке на дискретном скупу тачака х0 ,...,хп ,

f(xk)=g(xk), k=0,… ,n

тај облик апроксимације се назива интрполација. Тачке х0 ,...,хп су чворови интерплације. Ако се функција g(x) тражи у облику генерисаног полинома параметри интерполације се добијају решавањем система линеарних једначина
п
∑ сiφi(xk)=f(xk) k=0 ,… ,n .
i=0

Када је φ(x) у репрезентацији генерисаног полинома φк(х)≡хк , к=0,...,п интрполациона финкција g(x) се назива интерполациони полином,

n
Ln(x)=∑cixi .
i=0

Њутнов интерполациони полином са подењеним разликама:

Ln(x)=f(x0)+f[x0,x1](x-x0)+…+f[x0,…,xn](x-x0)∙∙∙(x-xn-1) .

Сматра се уопштењем парцијалне суме Тејлоровог реда функције f(x) .

Када су чворови хi равномерно распоређени са кораком h , хi=х0+ihкористимо коначне разлике. Разлика fi+1-fi=∆fi је разлика унапред.

Њутнов интерполациони полином за интерполацију унапред:

q(q-1) q(q-1)···(q-n+1)
Ln(x0+qh)=f0+q∆f0+————∆2f0+∙∙∙+————————∆nf0
2! n!

Њутнов интерполациони полином за интерполацију уназад:

q(q+1)∙∙∙(q+n)
f(x0+qh)-Ln(x0+qh)=—————————hn+1f(n+1)(ξ), x-n<ξ<x0
(n+1)! ¯ ¯

Њутнова метода за решавање једначина у R1

Нека је X≡Y≡R1, тј. оператор F је реална функција једне променљиве ƒ(х).
Алгоритам којим је дефинисана Њутнова метода је
ƒ(хп)
хп+1=хп- —— , п=0,1,...,
ƒ΄(хп)

уз услов да је ƒ΄(хп)≠0 за свако п.
Како је једначина тангенте на криву ƒ(х) у тачки хп

у=tn(x)≡ƒ΄(xn)(x-xn)+ƒ(xn),

очигледно је да је тачка хп+1 решење једначине tn(x)=0. Другим речима, на сваком кораку функција ƒ(х) се апроксимира својом тангентом у тачки (хп,ƒ(хп)), и нова апроксимација решења хп+1 као пресечна тачка ове праве са осом Ох. Зато се ова метода у једнодимензионом случају још назива и метода тангенте.
У модификацији Њутнове методе
ƒ(хп)
хп-1=хп- ——— , п=0,1,...
ƒ΄(х0)

у п-тој итерацији ƒ(х) се апроксимира правом која пролази кроз тачку (хп,ƒ(хп)), а паралелна је тангенти на криву у тачки (х0,ƒ(х0)) (сл.1).

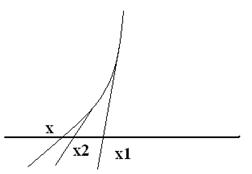
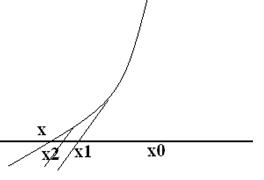
Услови конвергенције Њутнове методе у простору R1 су исказани следећом теоремом:
ТЕОРЕМА: Ако функција ƒ:[a,b]→R1 има следеће особине
(а) непрекидно је диференцијабилна,
(b) има различити знак на крајевима интервала [a,b], ƒ(a)ƒ(b)<0,
(c) за свако х из сегмента [a,b] постоји ƒ΄΄(х),
(d) на интервалу [a,b] ƒ΄(x) и ƒ΄΄(x) не мењају знак, и ƒ΄(х)≠0 за свако х
из интервала [a,b] ,
(е) тачка х0 из интервала [a,b] је таква да је ƒ(х0)ƒ΄΄(х0)>0,
онда низ {xn}, са првим чланом х0 и одређен формулом, конвергира ка
јединственом решењу х* из интервала [a,b] једначине ƒ(х)=0.

Оцена којом је потврђена квадратна брзина конвергенције Њутнове методе:
М2
| х*-хп|<—— |хп-хп-1| ,
¯ 2т1

т1= min |ƒ΄(x)|, M2=max |ƒ΄΄(x)|
x из интервала [a,b].

Њутн ненадмашив у чистој математици

У периоду између 1701-1702. Њутн је поново био представник у Парламенту,а 1703. године изабран је за председника Краљевског друштва. “Је ли Њутнов математички геније био мртав?”- свакако да не. Још увек је био једнак Архимеду. Али због случајног спречавања болести и сиромаштва, математичари су раса која интелектуално дуго живи. Њутн је и даље био интелектуално свеж. Њутн је лако могао сворити рачун варијација, инструент физичког и математичког открића који је одмах иза диференцијалног рачуна, уместо што је то оставио Бернулију и Лагранжу. Он је то напоменуо у делу Принципа када је одређивао облик површине окретања које се лепи кроз течност с најмањим отпором. Он је у главним цртама целу методу.
Бернулије и Лајбниц заједно су задали два изазова европским математичарима.
Први:”Замислимо две тачке случајно фиксиране у вертикалној равни.Који је облик криве доле коју мора честица начинити (без трња) под утицајем тежине када у најкраћем времену прелази од горње до доње тачке?’’
То је проблем “најкраћег времена”. Када је за њега чуо1696. године, Њутн је решио проблем (као и други) и дан пошто је чуо за њега,анонимно је саопштио решење Краљевском друштву. Није успео да сакрије свој идентитет. Када је видео решење Бернули је изјавио:”Ах! Препознао сам лава по његовим шапама.”. То није тачни превод са латинског.
Друга потврда Њутнове виталности догодила се 1716. године у његовој седамдесетчетвртој години. Лајбниц је пренагљено изнео оно што му се чинило као тежак проблем, изазивајући европске математичаре, наводећи посебно Њутна. Проблем је био да се пронађу ортогоналне путање било које врсте једнопараметарских криви. Њутн је проблем решио за једно вече. Лајбниц се надао да је овај пут нашао проблем нерешив за Њутна.
У читавој историји Њутн није имао супериорнијег (и можда ни једнаког) противника што се тиче способности концетрације свих снага свога интелекта за решавање проблема у једном тренутку.

Шта су други говорили о Њутну

Многи научници су цитирали Њутна као Библију, док је он о себи писао:
”Не знам како ме свет види,али себи самоме изгледам као дечак који се игра на морској плажи и, ту и тамо радује се када нађе по који гладак каменчић, или шкољку лепшу од осталих, а велики океан истине лежи сав неоткривен испред мене.”
Лајбниц је говорио да, ако узмемо математику од почетка света до времена Њутна, да је оно што је он урадио, боља половина.
Професор Мур(на Њутнов рад у периоду 1664-1665. године):
“У историји науке нема примера који се може упоредити са Њутновим успесима, до којих је дошао током те две златне године.”
Француски математичар Жозе-Луј Лагранж често је изјављивао да је Њутн највећи геније који је икада живео, додајући једном да је он, такође, и „најсрећнији, јер се систем света не може открити и установити више него једнога пута“. Енглески песник Александар Поуп, дирнут Њутновим постигнућима, написао је чувени епитаф:
Природа и природни закони у ноћној тами налазе скривеност;
Бог рече “Нека буде Њутн” и све постаде светлост.
(Nature and nature's laws lay hid in night;
God said "Let Newton be" and all was light.)

ЛИТЕРАТУРА

[1] Д. Ј. Стројк, Кратак преглед историје математике,Завод за уџбенике и наставна средства, Београд, 1991.

[2] Е. Т. Bell, Велики математичари, Знање, Загреб, 1972.

[3] C. B. Boyer, A History of Mathematics,Wiley, New York, Chichester, Brisbane,Toronto, 1968.

[4] Б. Симић, И ТО ЈЕ МАТЕМАТИКА,Завод за уџбенике и наставна средства, Београд, 1992.

[5] Д. Радуновић, Нумеричке методе, УНИВЕРЗИТЕТ У БЕОГРАДУ, Београд, 1998.

[6] http://sr.wikipedia.org/wiki

PROČITAJ / PREUZMI I DRUGE SEMINARSKE RADOVE IZ OBLASTI:

preuzmi seminarski rad u wordu » » »

Besplatni Seminarski Radovi