OSTALI SEMINARSKI RADOVI
IZ MATEMATIKE: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Geometrija horizonta
Ukoliko se nalazite na morskoj pučini ili na ravnom polju, u daljini ćete zapaziti liniju na kojoj se ,,nebo sa Zemljom sastaje.’’ Okrenete li se oko sebe, shvatićete da ste u centru kruga. Da li je taj krug realan? Postoji li zaista linija koju vidite? Pokušajte da joj priđete i proverite njeno postojanje. Verovatno se u to niko neće upuštati; svesni smo da joj ne možemo prići. Dok se krećemo prema njoj, ona se neprestano udaljuje. Međutim, to što je ne možemo nagaziti ili uhvatiti rukom, još nije dokaz da linije nema. ,,Iako je nedostižna, ona ipak realno postoji.’’ ,,Za svaku tačku sa koje se posmatra postoji određena granica dela Zemljine površine koji se iz te tačke vidi.’’\ Ta granica je linija horizonta. Ona se menja kroz različite atmosferske prilike, menja se i od mesta do mesta. Dovoljno je da samo jednom zakoračimo levo ili desno, i iako nam se čini da se vidik uopšte nije promenio, horizont će ipak biti neznatno pomeren. Ljude opušta pogled ka horizontu, ili ih pak nadahnjuje. Bez obzira da li se nalazimo na pašnjaku, moru, oranici, ili u pustinji, on uvek ostaje impresivan. Gledajući ka pučini, na primer, zapitate li se koliko je daleko najdalja tačka koju vidite. Nije teško izračunati udaljenost horizonta. Način na koji se to može učiniti biće naveden u daljem tekstu, ali on ne predstavlja osnovni problem kojim ćemo se baviti.,,U najranije doba ljudskog djelovanja čovjek je upoznavao pojedine činjenice koje su ga tek kasnije dovele do određenih zakonitosti. Prirodne su ga pojave očito impresionirale, osobito neke’’…\\ Te naročite pojave bile su uglavnom nebeske. Bile su retke, nezgodne za posmatranje i proučavanje, i samim tim teško objašnjive ili potpuno misteriozne. Zato su bile jednako privlačne i naučnicima i ,,običnim smrtnicima’’. Dok su jedni uporno tragali za racionalnim rešenjima, drugi su, zbog svojih ograničenih pogleda, ta rešenja olako pripisivali natprirodnim silama. ,,Ipak, postojalo je i mnogo takvih pojava koje su bile redovite. Čovjek se na njih privikao i one su tako bile obične. Morao ih je zapaziti jer je to bio dio njegova života.’’\\ Te pojave, iako možda jednako ,,neobjašnjive’’ kao i one retke, daleko manje su privlačile pažnju običnih ljudi. Svi su se na njih navikli i prihvatili ih takve kakve su. Ili se nisu ni trudili da ih rasvetle, ili su brzopleto donosili zaključke o onome što im se činilo strašno očigledno.
Jedna od takvih običnih i svakidašnjih pojava je linija horizonta. Vidimo je gde god se okrenemo, a da li smo o njoj dovoljno razmišljali da bi mogli da je objasnimo? Već smo videli šta je linija horizonta i pomenuli izračunavanje njene udaljenosti. Ali gde se ona nalazi u odnosu na posmatrača, od čega zavisi, šta na njoj zapravo vidimo? Ideja ovog rada je, upravo, da se ukaže na zablude vezane za prethodna pitanja.
Visina linije horizonta
Jedna od takvih zabluda je da linija horizonta uvek leži u visini očiju. Čak i kada se penjemo na veću visinu i ona se penje zajedno sa nama. Na primer, ako se posmatrač nalazi u avionu na dovoljno velikoj visini, izgledaće mu da svaka tačka na zemlji leži ispod linije horizonta. To je optička varka. Na sledećoj skici primetimo posmatrača koji stoji na ravnom zemljištu i posmatrača koji leti balonom.
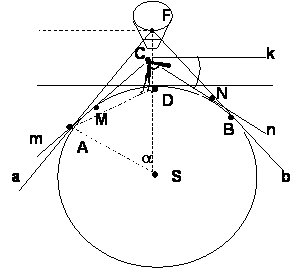
Slika 1. Spuštanje horizonta
U tački C nalazi se posmatračevo oko na
visini CD nad Zemljinom površinom. Vidni zraci imaju
pravce tangenti m i n koje u tačkama
M i N redom dodiruju krug koji nam u
ovom slučaju predstavlja deo Zemljine površine. Dakle, tačke M
i N su na liniji horizonta, odnosno pripadaju granici
vidljivog dela Zemljine površine. Dalje od tih tačaka Zemlja se nalazi
ispod vidnog zraka.
Oko drugog posmatrača nalazi se u tački F. Uočavamo da
je povećanje visine praćeno udaljavanjem linije horizonta. U ovom slučaju
tangente a i b poklapaju se sa vidnim
zracima, a tačke u kojima vidni zraci dodiruju Zemljinu površinu su A
i B, pa posmatrač ne vidi dalje od tih tačaka.
Specijalan slučaj je kada se oko posmatrača nalazi na visini koja je jednaka
nuli u odnosu na Zemljinu površinu. Tada se linija horizonta sažima u
tačku u kojoj se nalazi posmatračevo oko. (Neka je to tačka D
na našoj slici.) Do toga dolazi jer su vidni zraci tangente koje baš u
tački D dodiruju Zemljinu površinu. Ovaj slučaj je teoretski
moguć, ali u praksi vrlo redak. Čak i osoba koja leži na tlu posmatra
okolinu bar sa visine od 15 do 20cm. Jedino ako se posmatrač nalazi u
rovu ili nekom drugom udubljenju, ili pak u podmornici, njegovo oko može
biti na visini 0 iznad Zemljine površine. Zato ćemo ovog puta sve nestandardne
situacije zanemariti.
Zaključujemo da je linija horizonta uvek ispod nivoa očiju bez obzira
na visinu stajališta. Čak možemo definisati i ugao koji se zove ,,spuštanje
horizonta’’. Na našoj skici to bi bio oštar ugao koji poluprava k
(upravna na Zemljin poluprečnik u tački C) zahvata sa
pravom n (tangentnim vidnim zrakom). Zašto nam se onda
čini da je linija horizonta uvek u visini očiju?
Ovu optičku varku je odlično opisao i objasnio Edgar Alan Po u ,,Doživljajima
Hansa Pfala’’. ,,Pre svega, mene je začudilo to što mi se površina Zemlje
učinila udubljenom. Ja sam očekivao da ću je neizostavno videti ispupčenu
kad se budem peo uvis; tek sam razmišljanjem našao objašnjenje te pojave.
Vertikalna prava povučena od mog balona ka Zemlji činila bi katetu pravouglog
trougla čija bi osnovica bila duž od podnožja vertikale do linije horizonta,
a hipotenuza duž od linije horizonta do mog balona. Ali, moja je visina
bila ništavna u poređenju sa vidnim poljem; drugim rečima, osnovica i
hipotenuza zamišljenog pravouglog trougla bile su toliko velike u poređenju
sa vertikalnom katetom da sam ih mogao smatrati skoro paralelnim. Zato
svaka tačka koja se nalazi upravo pod letačem uvek izgleda da leži ispod
nivoa horizonta. Otuda utisak udubljenosti. I to će se produžiti sve dok
visina uspona ne postane toliko velika da osnovica trougla i hipotenuza
prestanu da izgledaju paralelne.’’\
Potrebno je možda objasniti nekoliko detalja iz ovog odlomka. Recimo,
vertikala o kojoj govori pisac, nije prava već duž FD
upravna na površinu Zemlje u tački D. Ona predstavlja
prvu katetu. Ono što je u tekstu nazvano osnovicom, zapravo je druga kateta.
Na našoj slici to je duž DA. Primetićemo, takođe, da
autor ugao ![]() FDA
tretira kao prav, iako on to nije. Ipak, za to ćemo naći realno opravdanje.
Ako sa S označimo središte Zemlje, tada je
FDA
tretira kao prav, iako on to nije. Ipak, za to ćemo naći realno opravdanje.
Ako sa S označimo središte Zemlje, tada je ![]() FSA
podudaran spuštanju horizonta u tački F. Veličinu tog
ugla možemo dobiti iz vrednosti kosinusa :
FSA
podudaran spuštanju horizonta u tački F. Veličinu tog
ugla možemo dobiti iz vrednosti kosinusa :
cos a = R/(R+h)
gde smo sa a obeležili ![]() FSA,
sa R poluprečnik Zemlje, a sa h visinu
na kojoj se nalazi oko posmatrača. Dobijamo da je ugao a
toliko mali da
FSA,
sa R poluprečnik Zemlje, a sa h visinu
na kojoj se nalazi oko posmatrača. Dobijamo da je ugao a
toliko mali da ![]() AFD
i
AFD
i ![]() ADF
možemo smatrati veoma bliskim pravom uglu.
ADF
možemo smatrati veoma bliskim pravom uglu.
Udaljenost horizonta
Pitanje ,,koliko je daleko horizont’’ suviše je uopšteno da bi smo na
njega mogli precizno odgovoriti. Naime, udaljenost horizonta zavisi od
velikog broja činilaca koji na nju bitno utiču. Neki od njih su: oblik
reljefa, visina stajališta, visina posmatrača, atmosferske prilike. Međutim,
ovaj problem možemo preformulisati, i dati mu oblik klasičnog, čak i jednostavnog,
geometrijskog zadatka.
Pretpostavimo da čovek prosečne visine stoji na ravnom zemljištu. Horizont
je tada krug u čijem se centru nalazi sam posmatrač. Da bi smo odredili
udaljenost horizonta, neophodno je naći poluprečnik pomenutog kruga.
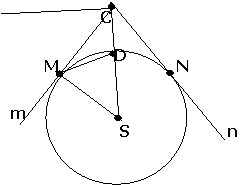
Slika 2. Udaljenost horizonta
Označimo sa S tačku koja nam na slici predstavlja središte Zemlje, a sa R Zemljin poluprečnik. Označimo sa C tačku u kojoj se nalazi oko posmatrača, sa D stajalište, a sa h visinu posmatračevih očiju u odnosu na tlo. Prave m i n su tangente iz tačke C koje dodiruju Zemljinu površinu u tačkama M i N. Zadatak se svodi na izračunavanje dužine duži CM, odnosno CN. Trougao CMS je pravougli sa pravim uglom kod temena M. Dužinu duži CM dobićemo primenjujući Pitagorinu teoremu.
CM²=(R+h)²-R²
=R²+2Rh+h2-R²
=2Rh+h2
CM²=h(2R+h).
Kako je visina posmatračevog oka veoma mala u odnosu na Zemljin prečnik, to umesto 2R+h možemo u izraz uključiti činilac 2R, bez bojazni da ćemo značajno izmeniti rezultat. Time će se i formula uprostiti:
CM²=2Rh
CM= . ![]()
Poluprečnik Zemlje iznosi 6378km, ali ćemo zbog jednostavnijeg računanja
u formulu uključiti R=6400km. Tada je
CM=![]()
CM=80 ·![]()
CM=113,14 . ![]()
Možemo smatrati da se udaljenost horizonta na Zemlji računa po sledećoj
jednostavnoj formuli:
udaljenost horizonta=113 ![]() (h je izraženo u kilometrima),
(h je izraženo u kilometrima),
a za udaljenost horizonta na bilo kom nebeskom telu važi sledeća formula:
udaljenost horizonta= ![]()
gde je R poluprečnik određenog nebeskog tela, a h
visina oka posmatrača. Ako pretpostavimo da se oko odraslog čoveka nalazi
na visini od 1.7m odnosno 0.0017km nad Zemljinom površinom, dobijamo da
je:
udaljenost horizonta=113 ![]() km
km
=4.66 km .
Ovaj račun je geometrijski veoma uprošćen, ali zato ne smemo zanemariti fizičke faktore koji utiču na udaljenost linije horizonta. Najvažniji među njima je atmosferska refrakcija. Prelamanje svetlosnih zrakova u atmosferi povećava udaljenost horizonta za 1/15 izračunate udaljenosti; možemo računati za oko 6%. Kada taj procenat dodamo rezultatu do kog smo prethodno došli, dobićemo preciznije rešenje:
4.66+0.06∙4.66=4.94km .
Dakle, odrastao čovek prosečne visine koji stoji na ravnom zemljištu,
vidi one tačke Zemljine površine koje su od njegovog stajališta udaljene
najviše 4.94km.
Međutim, taj broj od 6% je takođe samo prosek. ,,Udaljenost horizonta
se unekoliko uvećava ili umanjuje zavisno od mnogih uslova, i to se ona
| uvećava –pri visokom atmosferskom pritisku, –blizu Zemljine površine, –po hladnom vremenu, –izjutra i uveče, –po vlažnom vremenu, –nad morem; |
umanjuje –pri niskom atmosferskom pritisku, –na visini, –po toplom vremenu, –preko dana, –po suvom vremenu, –nad kopnom.’’ ([1] 139 st.) |
Kada se geometrija umeša u književnost…
Mnogi smatraju da se sa povećanjem visine stajališta, horizont veoma
brzo udaljuje. Tako su mislili, između ostalih, i Gogolj i Puškin.
Gogolj je, naime, u članku ,,O arhitekturi našeg doba’’ pisao sledeće:
,,Ogromne, kolosalne kule neophodne su u gradu… Kod nas se obično ograničavaju
na visinu koja omogućuje da se vidi samo grad, dok je za prestonicu
neophodno da se vidi bar na stopedeset vrsta\
unaokolo, a za to treba još samo jedan ili dva sprata više i sve će
se izmeniti. Vidik će se, srazmerno povećavanju visine zgrada, proširivati
neobičnom brzinom.’’ Lako ćemo izračunati koliko bi se vidik proširio
ovim nadziđivanjem koje predlaže Gogolj.
Ukupno povećanje udaljenosti horizonta iznosi 11.8%, a to je promena
koja se jedva zapaža.
Izračunajmo sada koliko visoku kulu bi trebalo sagraditi da bi se sa
njenog vrha moglo videti ,,bar na 150 vrsta unaokolo’’. Kako je 150vrsta
= 160km, postavićemo sledeću jednačinu:
160 = ![]()
1602= 2Rh
h = 1602/2R
h = 25600/12800
h = 2km .
Kula visine 2km potpuno je nerealna; to je pak visina jedne veće planine.
Svakako da Gogolj nije očekivao da kule o kojima piše moraju biti tako
ogromne.
Do ovakve greške neće doći ako se upitamo šta brže raste: visina uspona
ili udaljenost horizonta. Da bi smo dobili odgovor dovoljno je da pogledamo
formulu:
udaljenost horizonta = ![]() .
.
Udaljenost horizonta raste daleko sporije nego što se obično misli,
jer je proporcionalna kvadratnom korenu visine stajališta. ,,Kada se
visina posmatrača nad tlom uveća 100 puta, horizont se odmiče samo 10
puta dalje.’’
Puškin je u ,,Škrtom vitezu’’ ispričao jednu staru istočnjačku legendu:
,,Čitao sam negde
Da je car jednom neki vojnicima svojim
Naredio da po šaku zemlje bace na gomilu,-
I uzdigo se gordi breg
I car je s visine mogao veselo gledati
I dolinu belim šatorima pokrivenu
I more kojim galije brode’’.
Ako bi smo se samo malo udubili u stihove, primetili bi da je autor
nastojao da izazove divljenje čitalaca. Najpre je nameravao da istakne
brojnost careve vojske kroz sam način izgradnje brega. A potom je, nazivajući
breg ,,gordim’’, naglašavao njegovu impozantnu veličinu, čak toliku,
da su se sa njega mogli videti i dolina i more. Računski možemo proveriti
da li je priča zaista zadivljujuća.
U staro doba izuzetno brojnom smatrana je vojska od oko 100000 ljudi.
U tom slučaju ,,gordi breg’’ je bio napravljen od 100000 šaka zemlje.
Pretpostavimo da je zapremina šake oko 1/5 dm3, pa sledi da je zapremina
brega: 1/5 dm3 ∙100000 = 20000dm3 = 20m3 . Breg ima oblik kupe. Neka
je ugao koji zahvata izvodnica kupe sa osnovom jednak uglu prirodnog
pada, to jest 45o . Veći ugao bi izazvao preterano osipanje zemlje,
a manji ugao je čak i poželjan, jer je približniji stvarnoj situaciji.
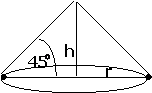
Slika 3. ,,Gordi breg’’
Ipak ćemo se zadržati na uglu od 45o . Tada je visina kupe h podudarna poluprečniku osnove r. Nađimo tu visinu iz formule za izračunavanje zapremine:
V = r2¶∙h/3 .
Kako su r i h podudarni, daćemo im zajedničku oznaku x= r= h . Formula će sada glasiti:
20 = x3¶/3
60 = x3 ¶
x3 = 60/¶
x = ![]()
x = 2.67m .
Moramo primetiti da se gomila zemlje visoka 2.67m teško može nazvati
,,gordim bregom’’. Ipak, izračunajmo koliko to uzvišenje utiče na proširenje
vidika. Neka je visina carevih očiju dok stoji na ,,gordom bregu’’
1.7m+2.67m = 4.37m = 0.00437km .
Udaljenost horizonta tada će biti:
![]() =
7.48km .
=
7.48km .
Uzmimo u obzir i uticaj atmosferske refrakcije:
7.48km∙1.06 = 7.93km .
Dobijamo da će car, stojeći na ,,gordom bregu’’, videti pri idealnim uslovima, oko 8km unaokolo, što je samo 3km dalje nego što bi video nepenjući se na breg. Zaključujemo da se vojni logor nalazio vrlo blizu obale. Puškin je očekivao da će izgrađeno uzvišenje značajno proširiti vidik, čak možda više desetina kilometara. Takva očekivanja u svakom slučaju pokazuju nepoznavanje odnosa između daljine horizonta i visine posmatračevog oka.
Brod na horizontu
,,Kada sa obale mora ili velikog jezera posmatramo brod koji se pojavljuje na horizontu, čini nam se da brod vidimo ne u onoj tački u kojoj se on stvarno nalazi već mnogo bliže, u tački gde naš vidni zrak klizi po ispupčenoj površini mora.’’\ Na slici 4, tačku u kojoj vidni zrak dodiruje površinu mora, označićemo sa T. To je najudaljenija tačka na Zemljinoj površini koju vidi posmatrač gledajući u pravcu broda. To što posmatrač ne vidi Zemljinu površinu iza tačke T, ne znači da se njegov vidik u tački T završava. Naime, on vidi svaki objekat koji preseče njegov vidni zrak, pa makar on bio i iza tačke T\\. Kada brod, krećući se od pučine ka obali, priđe dovoljno blizu, tako da se njegova najviša tačka nađe na vidnom zraku, u tom trenutku posmatrač prvi put uočava brod. Kako se Zemljina površina iza tačke T nalazi ispod vidnog zraka, nama se čini da se brod pojavljuje u tački T. ,,Ako posmatramo golim okom, teško se možemo oteti utisku da se brod nalazi’’\ na horizontu.
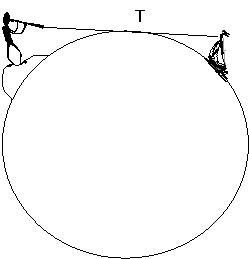
Slika 4. Brod na horizontu
,,Međutim, durbinom se taj podbačaj u oceni udaljenosti broda mnogo jasnije zapaža. Durbinom ne vidimo podjednako jasno i bliske i udaljene predmete; durbinom podešenim za daljinu bliske predmete vidimo rasplinuto, i obrnuto, durbinom podešenim za blizinu udaljene predmete vidimo u magli. Stoga, ako upravimo durbin (koji dovoljno uvećava) ka pučini i podesimo ga tako da jasno vidimo površinu vode, brod će se videti u rasplinutim konturama, otkrivajući na taj način svoju veću udaljenost od posmatrača (slika levo). Naprotiv, ako durbin podesimo tako da se oštro vide obrisi broda upola skrivenog iza horizonta, zapazićemo da je kod horizonta površina vode izgubila svoju pređašnju jasnost i da nam se ocrtava kao u magli (slika desno).’’\


Slike 5. i 6. Brod na horizontu posmatran kroz durbin
Ove zanimljive probleme vezane za pojam horizonta mogli smo da razjasnimo i neznajući koliko je zapravo linija horizonta udaljena od posmatrača. Međutim, pomoću formule koju smo izveli, lako možemo izračunati na kojoj udaljenosti d će posmatrač prvi put ugledati brod koji prilazi obali. Potrebno je samo da znamo visinu najviše tačke broda h1, i visinu posmatračevog oka h2. Tada je:
D = ![]()
Sastaju li se šine?
Ako se nalazimo na pravom putu ili pruzi i gledamo u daljinu, učiniće
nam se da se put, odnosno pruga, postepeno sužavaju. Ivice puta u daljini
će se približiti, svetiljke kraj puta smanjiti, a šine izgledaju kao da
će se sastati. Naravno, realno se ništa od toga ne dešava. Ali zašto imamo
taj privid?
Podudarni predmeti izgledaće nam različiti u zavisnosti od toga koliko
su od nas udaljeni. Predmete koji su daleko vidimo pod manjim vidnim uglom
nego njima podudarne predmete koji su blizu. Zato nam se daleki predmeti
čine manji. ,,Svaki predmet pretvara se pritom u jedva primetnu tačku,
premalu za čovečje oko, u mrlju bez dimenzija i oblika’’\
ako ga posmatramo pod uglom od 1’. Osobina normalnog
čovečjeg oka je da prestane da razlikuje konture predmeta ako ga vidi
pod ovim ili manjim uglom. Zato se taj ,,uglovni minut’’ naziva graničnim
minutom, ili srednjom granicom oštrine vida. Pitanjem: ,,Čime je uslovljena
ova osobina oka’’, bavi se fizika i fiziologija čula vida. Mi ćemo se
vratiti ,,geometrijskoj strani te pojave’’. Kada posmatramo izvesne objekte
golim okom na njima ne možemo primetiti sve detalje, ili pak ne uočavamo
ni same objekte. Ako posmatramo kroz mikroskop ili teleskop za koji kažemo
da uvećava 100 puta, mi te iste objekte vidimo pod 100 puta većim uglom.
,,I tada pojedinosti koje se od golog oka kriju iza granice oštrine vida
postaju pristupačne našem oku.’’\\
Lako možemo izračunati koliko je od nas udaljeno telo koje vidimo pod
uglom od 1’. Ustvari, mi računamo udaljenost od oka na kojoj telo gubi
svoj oblik i dimenzije, i postaje tačka. Tu udaljenost izrazićemo u funkciji
prečnika samog tela.
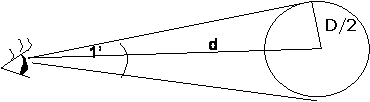
Slika 7. Vidni ugao tela i granični minut
Neka je rastojanje tela od oka posmatrača d = kD, gde je D prečnik tog tela. Tada je:
sin 0.5’ = D/(2d)
= D/(2kD)
= 1/(2k)
k = 1/(2∙sin0.5’)
k = 1/(2∙sin(0.5∙1/60))
k = 1/(2∙sin(1/120))
k ≈ 3438 .
Dakle, udaljenost tela prečnika D koje vidimo pod uglom
od 1’, iznosi 3438∙D . Tako, na primer, nećete raspoznati
lice čoveka na udaljenosti od 200m. Rastojanje između očiju čoveka iznosi
samo 3cm, pa se već na udaljenosti na oko 100m oči stapaju u jednu tačku.
Zanimljivo pitanje je: Možemo li videti tačku u kojoj se sastaju šine?
Analiziraćemo rešenje: Da bi došlo do spajanja šina, potrebno je da realan
razmak među šinama posmatramo sa tako velike udaljenosti, da vidni ugao
bude jednak 1’. Jedino pod tim vidnim uglom svi oblici se pretvaraju u
tačku, pa to važi i za prugu. Ako nam je poznat razmak između šina, nije
teško izračunati udaljenost te tačke. Problem je u tome da li je horizont
dovoljno daleko, odnosno da li se tačka stapanja nalazi ispred ili iza
horizonta.
Na našim prugama, širina normalnog koloseka iznosi 1.435m. Pretpostavimo
da se nalazimo na ravnom zemljištu, i da je pruga prava. Tada je udaljenost
tačke stapanja:
d = 3438∙1,435m ≈ 4933m ≈ 4.93km .
Udaljenost horizonta u ovom slučaju prethodno smo izračunali, i ona iznosi
4.94km. Zaključak je da možemo videti tačku spajanja šina.
Međutim, širina pružnog koloseka u Rusiji na primer, iznosi 1.52m. Pod
istim uslovima kao u prethodnom slučaju, šine će se sastati na udaljenosti:
d1 = 3438∙1.52m ≈ 5225m ≈ 5.22km .
Ta tačka se nalazi iza linije horizonta pa je ne možemo videti. Ona će postati vidljiva ako izmenimo uslove:
- Ako je oštrina vida posmatrača oslabljena, pa se za njega predmeti slivaju u tačku kad ih vidi pod izvesnim uglom većim od 1’.
- Ako pruga nije horizontalna.
- Ako se posmatrač nalazi na određenom uzvišenju.
Kod trećeg uslova potrebno je izračunati kolika je najmanja visina na
kojoj se može naći oko posmatrača, tako da on može da vidi spajanje šina.
Nju ćemo pronaći preko formule za udaljenost horizonta:
5.22 = ![]()
5.222 = 2Rh
h = 5.222/(2∙6400)
h = 0.00213km
h = 2.13m .
Ako želimo da nam udaljenost horizonta bude bar onolika kolika je udaljenost tačke spajanja šina, posmatračevo oko se mora naći bar na visini od 2.13m. U tom slučaju tačka spajanja šina biće na samom horizontu.
Horizont na Mesecu
![]() Formula
koju smo izveli za izračunavanje udaljenosti horizonta, biće valjana bez
obzira na kom se nebeskom telu nalazimo. Ona je uvek jednaka gde je h
visina očiju posmatrača, a R poluprečnik odgovarajućeg
nebeskog tela.
Formula
koju smo izveli za izračunavanje udaljenosti horizonta, biće valjana bez
obzira na kom se nebeskom telu nalazimo. Ona je uvek jednaka gde je h
visina očiju posmatrača, a R poluprečnik odgovarajućeg
nebeskog tela.
Ako bi smo se nalazili na nekoj Mesečevoj ravnici, udaljenost horizonta
bila bi jednaka:
![]() =
2.44km
=
2.44km
gde je 2R=3500km, a h=1.7m.
Na Zemlji nema takvih oblika reljefa koje bi smo mogli makar uporediti
sa reljefom Meseca. Reljef Meseca karakterišu takozvani prstenasti planinski
venci, a jedan od najvećih je Kopernikov krater. Njegov spoljni prečnik
iznosi 124km, a unutrašnji 90km. Najviša tačka bedema nalazi se na 1500m
visine u odnosu na dno kotline. Pokušaćemo da otkrijemo da li iz sredine
unutrašnje kotline možemo videti prstenasti greben.
Neka je a spoljašnji prečnik kratera, a=124km.
Neka je b unutrašnji prečnik kratera, b=90km.
Neka je H visina najviše tačke bedema, H=1500m=1.5km.
Neka je h visina očiju posmatrača, h=1.7m=0.0017km.
Potrebno je prvo izračunati udaljenost horizonta za greben bedema, odnosno
za visinu od 1.5km. Označimo je sa d1.
d1 = ![]()
d1 =![]() =
=
= 72.46km .
Zatim ćemo udaljenosti d1 dodati udaljenost horizonta na Mesecu za čoveka srednjeg rasta koji stoji na ravnom tlu. To je d2=2.44km koje smo prethodno izračunali.
d1 + d2 = 72.46km + 2.44km ≈ 75km
Dakle, 75km je najveća udaljenost sa koje bi čovek, stojeći u kotlini, mogao da vidi greben.
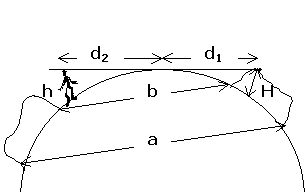
Slika 8. U Mesečevom krateru
Kako je centar kotline, u kome se nalazi posmatrač, udaljen od ruba kratera 45km, to je sasvim moguće videti greben iz centra kotline.
Mesec na horizontu
,,Matematika se tokom cele svoje istorije ne može odvojiti od astronomije’’…
,,Numerička astronomija je veoma napredovala na Istoku u epohi koja je
neposredno prethodila helenističkoj, i to naročito u Mesopotamiji u poznoasirskoj
i persijskoj epohi.’’ ,,Za matematičare je kretanje Meseca bio jedan od
najtežih, ali i najinteresantniji astronomski problem, i to kako u stara
vremena tako i u XVIII veku. Vavilonski (,haldejski’) astronomi uložili
su mnogo truda u ispitivanje Mesečevog kretanja.’’\
Među naučnicima XVIII veka koji su se posvetili ovom problemu, najistaknutiji
su Ojler i Njutn.
Međutim, mi se nećemo baviti niti efemeridama, niti problemom triju tela
Sunce, Mesec, Zemlja. Ukazaćemo samo na jednu neobičnu pojavu koja se
lako uočava posmatranjem Mesečevog kretanja sa Zemlje golim okom. Svako
od nas je mogao da primeti ,,da je pun Mesec, kad je nisko nad horizontom,
znatno veći nego kad stoji visoko na nebu. Razlika je toliko velika da
je teško ne zapaziti je. To je isto i sa Suncem: poznato je koliko je
veliki Sunčev kotur na zalasku ili u zoru’’.\\
Ova pojava je veoma zagonetna jer ,,nebeska tela, kad ih posmatramo pri
izlasku ili zalasku, ne samo da nam nisu bliža nego su čak dalja od nas
(za veličinu Zemljinog poluprečnika). To je lako razumeti iz sledeće slike:
u zenitu posmatramo nebesko telo iz tačke A, a na horizontu iz tačke B
ili C.’’\\\
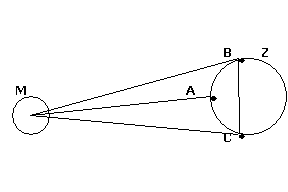
Slika 9. Mesec u zenitu i na horizontu
Zašto se
onda Mesec uvećava kad se približava horizontu? Nije dovoljno što smo
uočili problem. Potrebno je ,,objašnjenje, a ne samo registracija nebeskih
pojava.’’\\\\
Da bi smo došli do odgovora, izmerićemo vidni ugao Mesečevog kotura na
horizontu i u zenitu. Dobićemo uglove iste veličine, oko 30’. Ukoliko
se merenja vrše izuzetno preciznim instrumentima, pokazuje se da je vidljivi
prečnik Meseca ,,čak i manji kad se Mesec nalazi blizu horizonta usled
toga što se zbog refrakcije Mesečev kotur vidi nešto spljošten.’’\\\\\
Sada je već jasno da se radi o optičkoj varci. Iluzija smanjenja i povećanja
nebeskih tela prilikom njuihovog kretanja po nebeskom svodu, i postoji
zato što svod ,,ne izgleda kao polusfera u geometrijskom smislu reči već
kao sferna kalota (kapa) čija je visina dva do tri puta manja od poluprečnika
osnove. Do toga dolazi zato što pri običnom položaju glave i očiju za
horizontalna i njima bliska rastojanja stičemo utisak da su veća u poređenju
sa vertikalnim rastojanjima; u horizontalnom pravcu predmet posmatramo
pravo, a u svakom drugom podignutim ili spuštenim pogledom. Ako Mesec
posmatramo ležeći na leđima, on će nam, naprotiv, izgledati veći kad je
u zenitu negoli kad je nisko nad horizontom. Pred psihologe i fiziologe
se postavlja zadatak da objasne zašto vidljive dimenzije predmeta zavise
od naših očiju.’’\
Sledeća slika objasniće uticaj prividne spljoštenosti nebeskog svoda na
veličinu nebeskih tela u raznim njegovim delovim
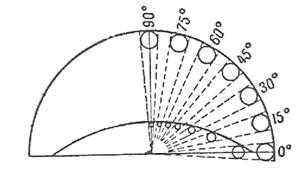
Slika 10. Uticaj spljoštenosti nebeskog svoda
,,Mesečev kotur uvek vidimo pod uglom od 30’, bilo da je Mesec na horizontu
ili u zenitu. Ali naše oko ne posmatra taj kotur uvek na jednom istom
otstojanju: Mesec u zenitu primiče nam se na manje otstojanje negoli kad
je na horizontu i zato nam njegova veličina kad je u ta dva položaja ne
izgleda ista – unutar jednog istog ugla krug (koji je upisan u taj ugao)
je manji što je god bliži temenu.’’\\
Postoji jednostavan način da se shvati da se Mesec na horizontu realno
ne uvećava. Tokom kretanja Meseca po nebeskom svodu ni u jednom trenutku
na Mesečevom koturu ne možemo uočiti neki detalj više, neku pojedinost
koja se u ostalim položajima Meseca ne vidi. To znači da nema uveličavanja
kakvo je moguće, na primer, gledanjem kroz dvogled, odnosno, nikad se
ne uvećava niti smanjuje vidni ugao pod kojim gledamo nebesko telo. Svako
drugo uvećanje je za nas ,,potpuno beskorisna optička varka.’’
Nekoliko reči za kraj
Dok smo još bili mali, i nismo znali da ćemo se u životu baviti matematikom,
čitali smo, ili su nam čitali, priču o Hajdi. U toj priči postoji jedan
veoma upečatljiv deo, bar je meni ostao u takvom sećanju, u kome Hajdi
tuguje. Dok je živela u gradu, sa prozora svoje sobe mogla je da vidi
samo ulice i krovove kuća. Zato je odlučila da se popne na ,,crkveni toranj
sa zlatnom loptom na vrhu’’ ne bi li odatle konačno ugledala brda, livade
i pašnjake, i dedinu kućicu. I sama sam tada očekivala da će na ovaj način
Hajdi zadovoljiti svoju želju. Međutim, Frankfurt, u kome je tada živela,
samo je 180km udaljen od planine Švarcvald na kojoj je bio njen deda.
Kada sam nedavno čitala knjigu J. Pereljmana ,,Zanimljiva geometrija’’,
i to baš odeljak o horizontu, setila sam se Hajdi. Problem koji je ona
imala, geometrijski je sasvim jasan, a neizvesnost u kojoj se nalazila
na žalost nije imala smisla. Ipak, razlog zašto sam odabrala ovu temu
nije da se obezvrede dečija nadanja, već me je, naprotiv, podstakla ta
tanka povezanost sa njima.
LITERATURA:
[1] J.PERELJMAN, Zanimljiva geometrija, Društvo matematičara, fizičara i astronoma SR Srbije, Beograd, 1978.
[2] ŽARKO DADIĆ, Razvoj matematike, Ideje i metode egzaktnih znanosti u njihovou povjesnom razvoju, Školska knjiga, Zagreb, 1975.
[3] KOLEKTIV AUTORA, Enciklopedija elementarne matematike za učenike škola II stupnja, Zavod za izdavanje udžbenika SR Srbije, Beograd, 1968.
[4] DIRK J. STROJK, Kratak pregled istorije matematike, Zavod za izdavanje udžbenika SR Srbije, Beograd, 1969.
preuzmi
seminarski rad u wordu » » »
